Systems
of Linear Equations
Graphing a system of two linear equations in the variables  and
and 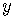

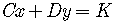 ,
,
we get two straight lines.
Solving the system means finding the point where the two lines intersect.
A point on the graph is given by two coordinate numbers
( first coordinate, second coordinate), so we need to determine these two numbers.
Several things can happen:
If the lines are parallel, they do not intersect. The system has no solution.
For example,
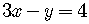
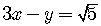 .
.
If the lines are coincident - one line lies on top of the other line -
then all the points on one line are also all the points on the other line.
The system has an infinite number of solutions.
For example,

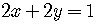 .
.
If the lines are not parallel and not coincident, then the lines intersect
in a unique point.
For example,

 .
.
There are two methods of solution - by elimination or by substitution.
In this section we will show
The Method of Substitution.
Here is the idea of the method, applied to the system above.
Step 1)
Pick one of the equations in the system, which one is not important.
To be specific, pick the first equation.

Note: Although, mathematically, which equation we pick is irrelevant -
we will get the same correct answer no matter which equation we pick
to start the process - it is best for us humans to pick the equation that
leads to the easiest algebra or arithmetic.
If we solve the equation for 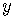 ,
we get
,
we get
 .
.
If we solve the equation for  ,
we get
,
we get
 .
.
This expression for  looks simpler than the expression for
looks simpler than the expression for 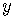
which involve a fraction and a minus sign.
Step 2)
Substitute this equation for  into the second equation of the system
into the second equation of the system
 ,
,
so
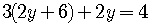 .
.
Solve this equation for 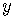 :
:
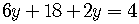 by the distributive property.
by the distributive property.

 to get
to get 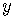 alone on the left side of the equation
alone on the left side of the equation
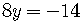 .
.
Now, divide by  to cancel that factor on the left side of the equation
to cancel that factor on the left side of the equation
and simplify the fraction that results on the right side of the equation.
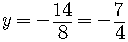
We have found the second coordinate of the point where the two lines intersect,
 .
.
What remains is to find the first coordinate, the value of the  .
.
Step 3)
Substitute 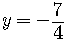 into
into  .
.
 .
.
Step 4)
Write down the point of intersection in coordinate notation.
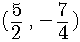
See Examples 1 - 2, pages 90 - 91.
top
next Linear
Inequalities