Straight
Lines
The graph of any equation of the form 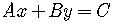
with 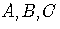 constants and
constants and 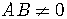 is a straight line.
is a straight line.
Any straight line in a rectangular Cartesian coordinate system
has an equation of this form.
From plane geometry we know that any two distinct points
uniquely determine a straight line.
So, to graph the equation of a straight line, we need to plot only two points
and then shoot a line through them and we are finished.
Intercepts of a straight line
Where the line intersects the x-axis is called the x -intercept,
where it intersects the y-axis is called the y-intercept.
For example,
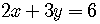 .
.
To find the x-intercept,
set 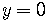 in the equation of the line and solve for
in the equation of the line and solve for 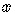 .
.
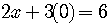
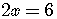
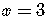
The x-intercept is 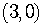 .
.
To find the y-intercept,
set 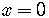 in
the equation of the line and solve for
in
the equation of the line and solve for 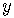 .
.
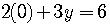
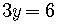
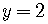
The y-intercept is 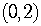 .
.
See Example 1, pages 192 - 193.
The Slope of a Line between two points 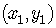 and
and 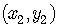
The slope m is given by
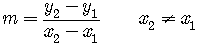
If the slope is positive, the line is rising, going from left to right.
If the slope is negative, the line is falling.
If the slope is zero, the line is horizontal.
If the slope is undefined, this corresponds to the denominator
in the above fraction being zero and the line is vertical.
See Table 1, page 194, and Example 2, pages 194 - 195.
Point-Slope Form
Consider the general problem of finding the equation of a straight line
passing though a given point 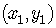 and having a given slope
and having a given slope 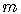 .
.
Look at any other point 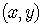 on the line.
on the line.
We can write an expression for the slope of the line between these two points,
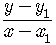 .
.
The slope of the line is given as 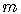 .
.
So, we can write the equation
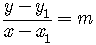 .
.
To get the standard form we want, just multiply the equation
by the denominator to get
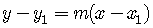 is the point-slope form.
is the point-slope form.
Slope-Intercept Form
When the given point is the y-intercept 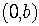 of the line,
of the line,
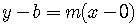
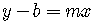
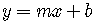 is the slope-intercept form.
is the slope-intercept form.
Remember, the intercept here is the y-intercept of the line, not the x-intercept.
This form is important because it says that if we write the equation of a line
in
this form, then the coefficient of the 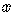 term on the right side of the equation
term on the right side of the equation
is the slope of the line.
Find the slope of 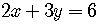 .
.
Solve for 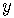 .
.
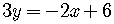
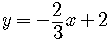
The slope is 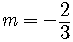 .
.
The y-intercept is 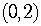 .
.
What is the x-intercept of the line?
We can not read from the equation the x-intercept the way we read the y-intercept.
We must go through the process of setting 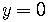 and solving for
and solving for 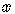 ,
,
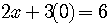 .
.
The x-intercept is 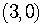 .
.
see Examples 3 - 5, pages 196 - 199.
Vertical and Horizontal Lines
The equation 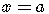 can
be rewritten to show the
can
be rewritten to show the 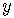 coordinate,
coordinate,
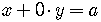 .
.
This says that no matter what value we assign to the 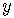 coordinate,
coordinate,
the 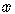 coordinate always has the given value
coordinate always has the given value 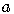 .
.
In other words, the line is always 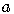 units from the y-axis.
units from the y-axis.
So
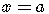
represents a vertical line.
Similarly, the equation
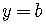
represents a horizontal line.
See Example 6, page 200.
Parallel and Vertical Lines
Given two distinct lines
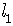 with slope
with slope 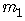
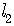 with slope
with slope 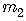 ,
,
the lines are parallel ( 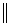 )
)
if and only if they have the same slopes,
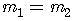 .
.
The lines are perpendicular ( 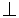 )
)
if and only if the product of their slopes is equal to negative one, 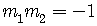
or equivalently,
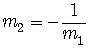 .
.
For example, if a given line has the slope 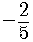 ,
,
then the the slope of any other line parallel to it is also 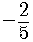 .
.
The slope of any other line perpendicular to it is
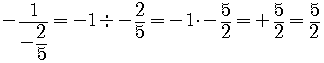 .
.
See Example 7, pages 201 - 202.
top
next Functions .
.