Exponential
and Logarithmic Equations
Use the properties of exponential and logarithmic functions
to solve equations involving these functions.
Exponential Equations
Example 1
Solve 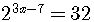 .
.
Note that 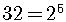 .
.
So the problem is the same as
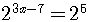 .
.
Since the exponential function is one-to-one,
the exponents must be equal to each other,
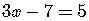 .
.
The solution is
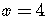 ,
,
which can be checked by plugging the number back
into the original equation.
Example 2
Solve 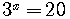 .
.
In this problem we can't similarly rewrite 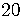 as a power of
as a power of 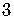 ,
,
so we have to use a different method to simplify the equation.
Take the natural logarithm or the common logarithm of both
sides of the equation.
To be specific, use the common logarithm.
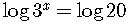
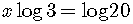 The logarithm of a power
The logarithm of a power
is the power times the logarithm.
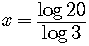 .
.
If we want a numerical answer, we can use a calculator
to find the values of the common logarithms,
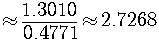 .
.
Using the natural logarithm we would get the same numerical answer
with a calculator. But if we used logarithms to any other base, say, 13,
we could not so directly get a numerical answer.
Example 3
Solve 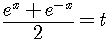 for
for 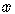 .
.
Multiply both sides of the equation by 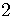 to cancel
to cancel
the fraction on the left side of the equation,
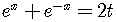 .
.
Rewrite using positive exponents,
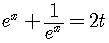 .
.
Multiply by 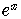 to cancel the fraction on the left side,
to cancel the fraction on the left side,
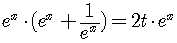
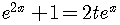 .
.
Rewrite the equation so the right side or the left side of the equation
is zero. Which side is not important.
To be specific, put the zero on the right side.
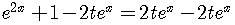
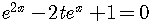
This equation is reducible to a quadratic equation
because it can be rewritten as
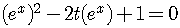 .
.
The substitution 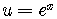 renders the equation equivalent to
renders the equation equivalent to
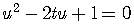 .
.
Using the quadratic formula with 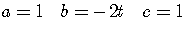 ,
,
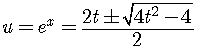
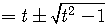 .
.
Finally, to get 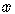 alone, take the natural logarithm
alone, take the natural logarithm
of both sides of the equation,
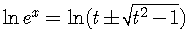 .
.
Remember that 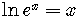 .
.
The solution is
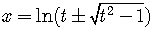 .
.
See Examples 1 - 4, pages 395 - 398.
Logarithmic Equations
Example 4
Solve 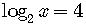 .
.
By using the definition of a logarithm, rewrite the equation
as an exponential equation,
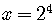
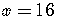 .
.
Example 5
Solve 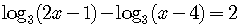 .
.
The difference of logarithms is equal to the logarithm of a quotient,
so the left side can be rewritten as
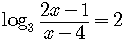 .
.
Rewrite this as an equivalent exponential equation.
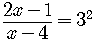
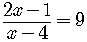
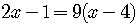
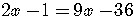
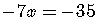
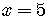
Remember always to check the number in the original logarithmic equation.
It may work or it may not. In this case, it works.
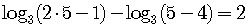
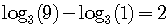
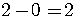
is true so 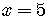 really is the solution.
really is the solution.
See Examples 5 - 7, pages 398 - 400.
Change of Base Formula
Sometimes we need to change the base of a logarithm.
For example, to find the numeral value of 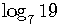 ,
,
rewrite it in terms of common logarithms or of natural logarithms.
Then we can easily compute the value with a calculator that has
 or
or  buttons.
buttons.
Generally, we want to write 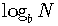 in terms of
in terms of 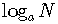 ,
,
where 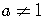 ,
,
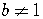 , and
, and
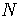 are arbitrary
positive numbers.
are arbitrary
positive numbers.
Let
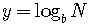 .
.
Rewrite this in exponential form.
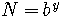
Take 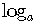 of both sides of the equation.
of both sides of the equation.
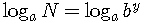
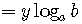 by the power rule for logarithms.
by the power rule for logarithms.
Solve this equation for 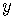 .
.
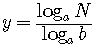
But 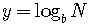 .
.
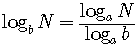 is the change-of-base formula.
is the change-of-base formula.
So, in terms of common logarithms we can compute
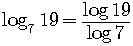 .
.
See Example 8, pages 400 - 401.
top
next Sequences
and Series
Module
6