Sequences and Series


Sequences
A simple example of a sequences is
     
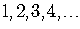
The three dots at the end indicate that the sequence goes on forever.
To completely determine the sequence, a formula that tells how to
calculate the terms, or elements, of the sequence must be give.
In this example, the formula is
     
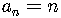
where is the position of the term in the sequence.
For the first term,  ,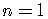
so   .
For 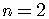 ,  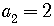 , and so on.
For the 100^th term of the sequence, 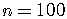  , so   .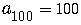

A sequence is represented in general by
     
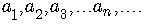
where 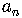   is the general term of the sequence.
It is the formula that tells us how to calculate the terms of
the sequence and it must be given in order to specify a unique sequence.
If the sequence goes on forever , the sequence is called an
infinite sequence.
If the sequence stops after a certain number of terms, it is called a
finite sequence.

Sometimes, the general term of the sequence is a formula that gives an
element of the sequence in terms of other elements of the sequence.
Such a formula is called a recursive formula.
A famous example of such a sequence is the Fibonacci sequence:
     
     
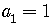
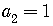
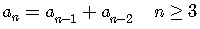         is the recursive formula
                                                           for the general term.

The elements of a sequence are
     
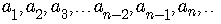
The recursive formula gives the value of the n-th element in terms
of the (n-1)-th element and the (n-2)-th element; in other words,
the value of an element is given as the sum of the previous two
elements in the sequence.
     
     
     

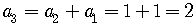
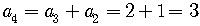
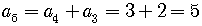
The Fibonacci sequence, then, is
          
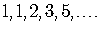
See Examples 1 - 2, pages 798 - 799.


Series
If we add all the terms of a sequence, we get an expression
that is called a series,
     ,
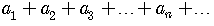an infinite series if the terms go on forever, a finite series
if the terms stop after a certain number of them.
The summation notation makes it easy to write a series
in compact form.

Example


See Examples 3 - 4, pages 801 - 802.


                       top
                       next     Mathematical Induction