Binomial
Formula
Factorial
For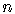 
a natural number, the factorial is the product of the first
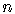natural numbers.
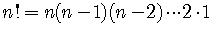
In particular,
.
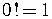Notice that we can group factors and write
.
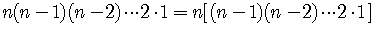The product within the brackets is 
Therefore, we have the
Recursion Formula
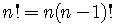
See example 1, page 826.
Combinatorial Symbol
For nonnegative integers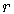 
and 
,
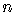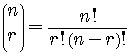
Other notations for the combinatorial symbol are
,
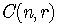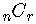, or
.
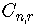These symbols are also called binomial coefficients.
See Example 2, page 827.
Binomial Formula
For 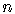a positive
integer
.
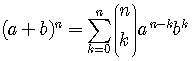Observations
1)
The expansion of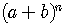 
has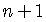 
terms.
2)
As we move from the left of the expansion to the right of the expansion,
the powers of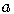 
decrease and the powers of 
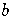increase.
3)
In each term, the sum of the powers o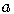f and
of 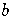always
add up to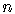 
.
Example 1
The number of terms in the expansion is 5+1.
As the powers of a decrease from 5 to 1, the powers of b
increase from 1 to 5.
In each term, the sum of the powers of a and b always
add up to 5.
Example 2
Expand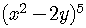 
.
In the binomial formula let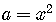 
,
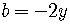, and
.
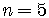Evaluate the binomial coefficients and do the algebra.
See Examples 4, page 830.
Suppose we want to determine only a particular term in an expansion.
The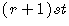 
Term of the Binomial Expansion 
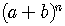is
.
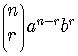Example 3
Find the 5th term in the expansion of
.
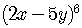We must write the number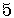 
so it is
in the form,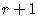 
,
given in the formula.
,
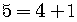so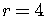 
.
The other substitutions are
,
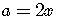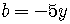, and
.
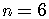Then the 5th term in the expansion is
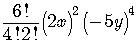or
or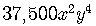 
.
See Example 5, page 831.
top
next Multiplication
Principle, Permutations and Combinations
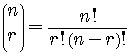
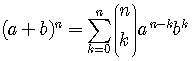
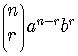