Mathematical
Induction
The Principle
Let 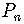 be a statement associated with each positive integer
be a statement associated with each positive integer 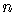
and suppose the following conditions are established:
1)
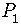 is true
is true
2)
For any positive integer, if 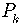 is true then
is true then 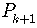 is
also true.
is
also true.
Then the statement 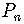 is true for all positive integers
is true for all positive integers 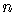 .
.
The idea of mathematical induction is first
to established that the result is true for a single case
and second
to establish that if it is true for some value of 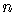 ,
,
then it is also true for the next higher value of 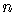 .
.
These two results serve to establish that the result
is true for all values of 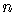 .
.
The second step takes the particular result of the first step
and establishes it as a general result, not particular only for
a given value but true for all values.
Example
Suppose we have to prove that the sum of the cubes of the first
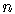 natural
numbers is equal to
natural
numbers is equal to
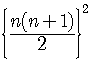 .
.
In other words, is the formula
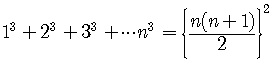
true for all values of 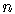 ?
Is the formula always true?
?
Is the formula always true?
Step 1)
Check the formula for a particular value of 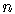 .
.
For 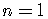 .
.
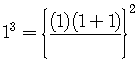 Is this true?
Is this true?
Work out the right side of the equal sign sign.

The left side of the equal sign is 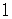 and the right side of the equal sign is
and the right side of the equal sign is 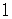 .
.
So we have the relation
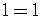 which is true.
which is true.
Let us check for 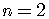 .
.
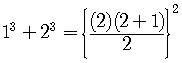 Is this true?
Is this true?
The left side is
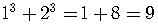 .
.
The right side is
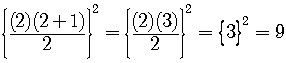 .
.
So we get the statement
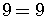 which is true.
which is true.
Let us check for 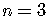 .
.
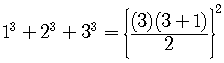 Is this true?
Is this true?
The left side is
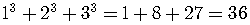 .
.
The right side is
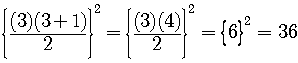 .
.
So we get the statement
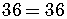 which is true.
which is true.
Step 2)
Establish the induction,
true for 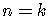 implies true for
implies true for 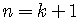 .
.
Assume the formula is true for 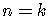 .
.

Add the (k+1)th term, that is, 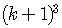 ,
to both sides,
,
to both sides,
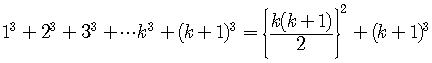 .
.
Now, work out the right side.


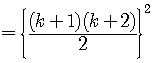 , which
is the same form as the result
, which
is the same form as the result
we assumed to be true for 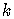 terms,
terms, 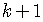 taking
the place of
taking
the place of 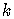 .
.
In other words, if the result is true when we take a certain number of terms,
whatever that number may be, it is true when we increase the number by one;
but we see that it is true when 3 terms are taken; therefore, it is true when
4
terms are taken; it is therefore true when 5 terms are taken; and so on.
So the result, the formula, is true for all values of 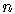 .
.
The formula is always true.
Other such formulas are

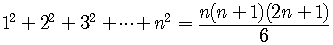
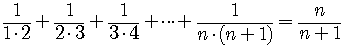 .
.
All are proved using mathematical induction.
See Examples 1 - 3, pages 806 - 810.
top
next Arithmetic
and Geometric Sequences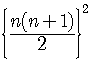 .
.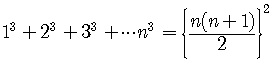
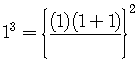 Is this true?
Is this true?
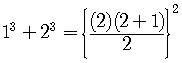 Is this true?
Is this true?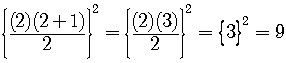 .
.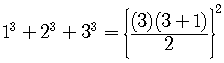 Is this true?
Is this true?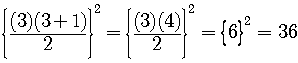 .
.
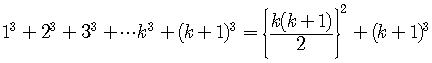 .
.

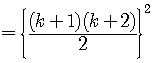 , which
is the same form as the result
, which
is the same form as the result