Lengths of Plane Curves
Arc Length Formula
Dealing with Discontinuities in the Derivative
The Short Differential Formula
Parametric Arc Length Formula

Lengths of Plane Curves
We approximate the length of a curve by the length of polygonal line segments
that closely follow the shape of the curve. We can not directly measure the length
of a curve but we can easily measure the length of a straight line segment.
We replace a hard problem by an easier problem.
As we go to the limit, that is, simultaneously let the number of line segment
approximations (the partition) go to infinity and the distance between any
two adjacent points along the curve (the norm) go to zero, the approximations
tend in the limit to the exact value of the length of the curve.
We are talking, again, about Riemann sums and their limit which is the
definite integral.



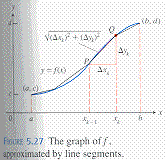
The triangle in the above figure is a right triangle with the hypotenuse  PQ.
The length of  PQ  approximates the length of the arc  PQ  of the curve 
.
The closer together the points  P  and  Q  are, the better the approximation.
By the Pythagorean Theorem,

.

With a little bit of algebra,

.

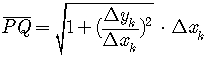By the Mean Value Theorem for differentiable functions,

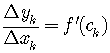   for some point  in the   subinterval  ,
                              so we can write

.

We approximate the length of the curve with the Riemann sum


We assume that    is continuous on  .
A function with this property that the derivative of the function is continuous
is said to be smooth on the closed interval.
In the limit, we get the exact value of the length of the curve.

Arc Length Formula for the Length of a Smooth Curve  

(1)   .

In this formula we integrate with respect to  .
Integrating with respect to  , a similar formula applies:
If    is smooth on  ,  the length of the curve
  from    to   is

(2)   .

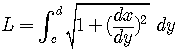See Example 1 - 4, pages 414 - 419.

Dealing with Discontinuities in the Derivative
Sometimes
  may fail to exist, but the inverse   may be okay.
         Then we may use Formula (2) above.

See Example 3, page 417.


The Short Differential Formula
Thinking of the derivatives as quotients of differentials, we can write

.

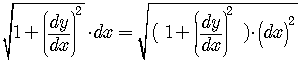Applying the Distribute Law,

                           

                           .

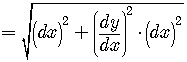
So, in terms of differentials, we can write the formulas
for the length of a curve in the condensed form



 and   would be expressed in terms of a common variable
and the limits of integration would be given in terms of this common
variable.
This is brought out explicitly in the

Parametric Arc Length Formula
If a curve
 is a given by parametric equations
                                                         ,  ,  ,
where    and   are continuous and not simultaneously zero on  ,
and if   is traversed exactly once as    increases from    to  ,
then the length of    is

.


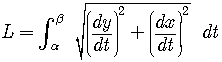See Example 4, page 419.


          next     Springs, Pumping, and Lifting
                      Top