Work Done by a Variable Force Along a Line
Work Done by a Constant force
Hooke's Law for Springs
Pumping Liquids from Containers

            Springs, Pumping, and Lifting

Definition of Work
The work done by a variable force
 directed along the x-axis from    to    is
.

If the force is constant, then the work is just force times distance,
.
The integral is not need.
If the force is variable along the distance, then the integral is needed.

See Example 1 - 3, pages 422 - 424


Hooke's Law for Springs
The force it takes to stretch or to compress a spring    l  length units from its
natural, unstressed length is
.
                     is the force constant characteristic of the spring.

See Example 4 - 5, pages 424 - 425.


Pumping Liquids from Containers



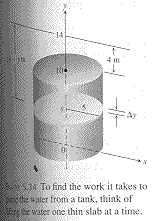
How much work does it take to pump all or part of the liquid from a container?
Imagine lifting the liquid out one thin horizontal slab, or disk , at a time and apply
the work equation

to each slab.
This, again, is the typical calculation we've seen many times before that leads
to a definite integral.
The particular integral depends on the weight of the liquid and the dimensions
and shape of the container, but the way we set up the definite integral is always
the same.

See Example 6 - 8, pages 425 - 428.

          next     Fluid Forces
                     Top