Derivative Rule for Inverses
Definition of the Natural Exponential Function
Properties
The Derivative
The Integral
e Expressed as a Limit
Definition of the General Exponential Function
The Power Rule (Final Form)
The Derivative of
The Integral of


                        Exponential Functions

The Derivative Rule for Inverses
If   is differentiable at every point of an interval    and     is never
zero on  , then    is differentiable at every point of the interval  :
.

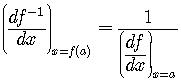See Examples 1 - 2, pages 467 - 468.


Definition of the natural exponential function 
The natural exponential function is defined as the inverse of the natural
logarithmic function, for any real number
.
In particular,
.
is not a rational number. Later, we will define it as a limit which
can be used to compute its value.

Properties



The Derivative of
The exponential function is differentiable because it is the inverse
of a differentiable function - the natural logarithmic function - whose derivative
is never zero.
If is a differentiable function of , then
.

See Example 3, page 470.

The Integral of 
The formula for the derivative of the exponential function immediately
gives the antiderivative
.

See Examples 4 - 5, pages 470 - 471.
Example 5 is an initial value problem.

e Expressed as a Limit


e is an irrational number, an infinitely non-repeating decimal.
Using a calculator, we can approximate it to 15 decimal places,
.

Definition of the General Exponential Function 
For any numbers   and  ,
.

See Example 6, page 472

The above definition for a general exponential function allows us
to define exponents for any real value of the exponent, rational
or irrational. Previously, we had defined exponents only for the
case where it is a rational number.
Now for any    and any real number  ,  rational or
irrational, we can write
.
So

            .
Generalizing by the Chain Rule, we have
The Power Rule (Final Form)
If    is a positive differentiable function of    and   is any real number,
then    is a differentiable function of    and
.

See Example 7, page 473


The Derivative of  .
If   , using the definition  , we can proceed as we did
above for the Power Rule:



            
            .

Generalizing by the Chain Rule,
If    and   is a differentiable function of  , then

.

See Example 8, page 473


The Integral of
The above derivative formula immediately gives the antiderivative formula
.

See Example 9, page 474


          next     Derivatives of Inverse Trigonometric Functions; Integrals
                     Top