Derivative of the Arctangent
Derivative of the Arcsecant
Derivatives of the Other Three
Integration Formulas
Completing the Squares
Derivatives of the Inverse Trigonometric Functions; Integrals
Inverse trigonometric functions appear in mathematics, engineering, and physics.
Derivative of the Arcsine
See Example 1, page 478.
Derivative of the Arctangent
See Example 2, page 479.
Derivative of the Arcsecant
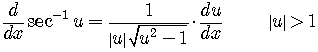
See Example 3, page 480.
Derivative of the Arccotangent
See Example 4, page 480.
Derivative of the Arccosecant
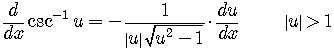
Derivative of the Arccosine
Integrals
The above six formulas for derivatives yield corresponding formulas
for antiderivatives.
See Example 5 - 9, pages 481 - 483.
Completing the Squares
Examples 7 and 8 use the process of completing the squares to get
the integrand into a form matched by a formula.
Recall how to complete the squares:
Let's do that part of Example 8.
Find
.In order to use the arctangent formula above, the denominator
must be in the form
.Completing the squares works only when the coefficient
of the quadratic term is
.
Factor out the 
:
.Now complete the squares inside the parenthesis:
Take
the coefficient of the linear term 
and square it
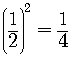
This is the number we must add inside the parenthesis in order to
make the expression inside the parenthesis a perfect square.
But this number was not there before, so in order not to change the
numerical valuation of the denominator we must also subtract away
from the denominator.
In effect, then, we have only added zero to the denominator,
which does not change the denominator's numerical evaluation.
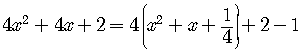
The polynomial in the parenthesis is now a perfect square,
which is the goal of completing the squares.
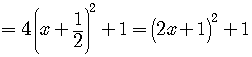.Then
( Let
,
so 
)
.Here
in the arctangent formula
.next First-Order Separable Differential Equations
Top