Definition of the Natural Logarithm Function
Laws for Logarithms
The Range
The Derivative                       Logarithmic Differentiation
The Integral of 1/u
Integrals of Tan x/Cot x
Derivative of  log_a u
Integrals Involving  log_a x

Definition of the Natural Logarithmic Function

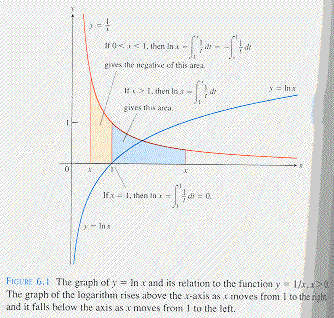
From the graph, we see that the function    is not defined for  .

By the Fundamental Theorem of Calculus, Part 1,



Generalizing by the Chain Rule, we get
The Derivative

                  (1)

where is a differentiable function of  .

See Example 1, page 459.


The usual Laws for Logarithms hold:
For any numbers    and  ,
i]
     

ii]
     

iii]
     

The Range
  and  


The Integral of
Equation (1) gives the corresponding antiderivative formula

                               (2)

which is true whether is positive or negative, but not zero.

Notice that this result fills in the exception in the Power Rule formula
.
When ,
,
which is just the integrand in formula  (2).

See Example 2 - 3, pages 461 - 462.


The Integrals of the Tangent and Cotangent
Using the substitution
,
,
we can write




.

A similar derivation works for .
Generalizing, when is a differentiable function

          (3)

            (4)

See Example 4, page 462.


Logarithmic Differentiation
If we want to differentiate a positive function consisting of products, quotients,
and powers, often a good way is to first take the logarithm of both sides
- using the laws of logarithms (i) - (iii), this step simplifies the function -
and then differentiating.

See Example 5, page 463

Derivative of
We use the change of base formula to write

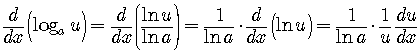     (5)

See Example 6, page 463.

Integrals Involving
First, convert the base   logarithms to natural logarithms, using the change of base formula.

See Example 7, page 464.

          next      Exponential Functions
                      Top