Indeterminate Form

Indeterminate Forms

Indeterminate Forms

Euler's Constant

             L'Hopital's Rule

Theorem 1 First Form                        Indeterminate form   
Suppose that

  and      exist and   ,
Then
.

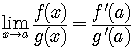See Example 1, page 578.

Sometimes the fraction on the right side is also indeterminate.
Then we need
Theorem 2 Stronger Form
Suppose that


 and    are differentiable on an open interval    containing  ,

  on      if    ,
Then
,
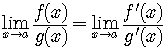assuming the limit on the right side exists.


This enables us to apply L'Hopital's Rule repeatedly, when applicable.
The   may itself be finite or infinite and may be an endpoint of the interval 
of Theorem 2.

See Example 2 - 4, pages 579 - 580.
When applying the Rule, watch for a change from

to something else, then stop applying the Rule.
Example 3 shows an incorrect application of the Rule.

Indeterminate forms                       
If
  and   both approach infinity as  ,
then
,
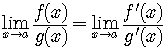provided the limit on the right side exists.
The   may itself be finite or infinite and may be an endpoint of the interval 
of Theorem 2.

By using algebra, the forms    and    may be transformed
to the form
  o r ,
then we can apply L'Hopital's Rule.

See Examples 5 - 7, pages 580 - 582.

Indeterminate Forms    Using Ln
These types of limits often can be worked out by first taking logarithms ,
using L'Hopital's Rule to find the limit of the logarithms, and then
exponentiating to get the limit of the original function.
The principle is:
If
,
then
,

can be finite or infinite.

See Example 8 - 10, pages 582 - 584.

Example 8 shows that
Euler's Constant
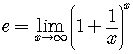, which can be used to compute the value.


         next     Improper Integrals
                    Top