The Fundamental Theorem, Part 1
The Fundamental Theorem, Part 2
The Mean Value Theorem
A continuous function on a closed interval assumes its average value
at least once in the interval. More precisely, if
is continuos on
such that
The theorem is not true if the function is not continuous in the closed interval.
A discontinuous function need not assume its average value.
For the function
There is no point
See Example 1 - 2, pages 352 - 353.
Definite integrals can be used to define functions.
defines
The value of the function depends on the value of the upper limit of integration.
Example
1]
Note that
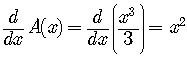 .
.appearing as the upper limit of integration. When we take the derivative of
In fact, this result is generally true!
The Fundamental Theorem of Calculus, Part 1
If
is a continuous function on
has a derivative at every point
We can put this result in another way:
For every continuous function
the differential equation
The solution can be written as a definite integral.
Example
2]
Though we do not know how to evaluate the definite integral, we can write down
its derivative.
3] Using the Chain Rule.
If
let
See Examples 3 - 6, pages 354 - 356.
Now we will evaluate definite integrals using antiderivatives.
The Fundamental Theorem of Calculus, Part 2
If
This result often makes the calculation of definite integrals much easier.
If we know the antiderivative, we do not have to calculate the limit of
Riemann sums.
Example
4]
Find
Using the definition of a definite integral as a Riemann Sum,
we would have to calculate
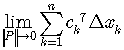 ,
,which would be not too easy.
But we know the antiderivative
so
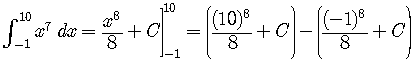
Much easier!!
See Examples 7 - 9, pages 359 - 361.
next Substitution in Definite Integrals
Top