Area Between Curves
Substitution in Definite Integrals
Substitute
,
, and integrate from
to 
.Example
1] Find
.The method of substitution works by being able to identify appropriate factors,
or parts, of the integrand so that by an equally appropriate renaming of those
parts, and the resulting symbolic simplification of the integrand, we can apply a
suitable known integral formula, or integration process, by which the integration
can then be carried to completion.
In the experimental process of trying to find a substitution that might work, it is
often fruitful to look at the most complicated grouping in the integrand. Sometimes,
there are several choices. Try one, see if it works, if it doesn't work, try another.
First, try
, then 
.In terms of
so
the integrand is
.This is good because we can use the power rule
to find the antiderivative.
But wait - the integration limits are in terms of the original variable,
and
.These limits can be given in terms of the new
variable.That is easy to do.
The lower limit
corresponds to 
.The upper limit
corresponds to
.
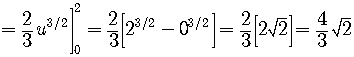
In this example, we went from the
variable
to the
variable, wrote everything in terms of
,
including the limits of integration.Another way is to leave everything in terms of the original
variable, including the limits of integration.
An intermediate step involves using the power rule, and then writing the result
of the power rule back in terms of
.
( But
)
.So
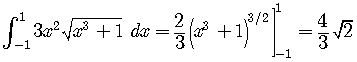.See Examples 1 - 3, pages 365 - 366.
Area Between Curves
If
and 
are continuous with
throughout
, then the
area of the region between the curves
and
from
to
is the integral
of 
from
to :
See Examples 4 - 5, pages 368 - 370.
next Numerical Integration
Top