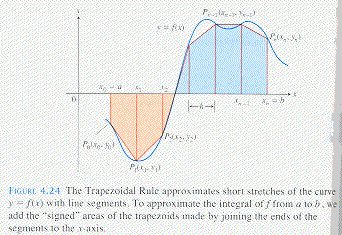
The Trapezoidal Rule approximates the area under a curve by using
trapezoids, summing the areas of all the trapezoids.
The
Trapezoidal Approximation Trapezoidal Rule
Error in the Trapezoidal Approximation
Approximation using Parabolas-Simpson's Rule
Error in Simpson's Rule
Which Rule Gives Better Results?
Round-off Errors
Numerical Integration
Trapezoidal Rule

The Trapezoidal Rule approximates the area under a curve by using
trapezoids, summing the areas of all the trapezoids.
![]()
The ![]() are the values
of the function
are the values
of the function ![]() at the partition points
at the partition points
![]() ,
, ![]() ,
,
![]() , . . . ,
, . . . ,![]() ,
,
![]()
where ![]() is the
step size.
is the
step size.
See Example 1 - 2, pages 374 - 375.
Error Estimate for The Trapezoidal Rule
If
![]() is continuous
and
is continuous
and ![]() is any
upper bound for the value of
is any
upper bound for the value of
![]() on
on
![]() , then
, then
![]() ,
,
where
![]() is
the step size.
is
the step size.
![]() is
the error in the Trapezoidal Approximation
is
the error in the Trapezoidal Approximation ![]() .
.
Simpson's Rule
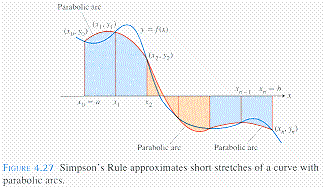
Simpson's Rule approximates the area under a curve by using parabolas,
summing the areas of all the parabolas.
![]()
The ![]() are the
values of
are the
values of ![]() at the partition points
at the partition points
![]() ,
, ![]() ,
,
![]() , . . . ,
, . . . ,![]() ,
,
![]()
The number ![]() is
even and
is
even and
![]() is
the step size.
is
the step size.
See Example 4, page 378.
Error Estimate for Simpson's Rule
If
![]() is continuous
and
is continuous
and ![]() is any
upper bound for the value of
is any
upper bound for the value of ![]()
on ![]() ,
then
,
then
![]() ,
,
where
![]() is
the step size.
is
the step size.
![]() is the error in the Simpson Approximation
is the error in the Simpson Approximation ![]() .
.
See Example 5, page 379.
Which Gives Better Results?
Compare the error estimates for the two approximations
![]() for
the Trapezoidal Rule
for
the Trapezoidal Rule
![]() for Simpson's Rule.
for Simpson's Rule.
The M's mean different things. The factors are different.
Ultimately, we have to look at the geometry of the curve
![]()
to see whether trapezoids or parabolas, if either, are going to give the better
result.
See Example 6 - 7, pages 379 - 380.
Round-off Errors
Decreasing the step size ![]() reduces the error in both Approximation Rules
reduces the error in both Approximation Rules
in theory. But in practice it may fail to do so. When ![]() is sufficiently small,
is sufficiently small,
round-off errors in the arithmetic required to evaluate the approximations may
so pile up that the error formulas no longer describe what is really happening.
Reducing ![]() below
a certain size can, in fact, make the approximations worst.
below
a certain size can, in fact, make the approximations worst.
next Volumes
by Slicing and Rotation About an Axis Module 2
Top Applications
of Integrals