Riemann Sums and Definite Integrals
Average (Mean) Value of a Function
Rules for Definite Integrals


Riemann Sums and Definite Integrals
Given the continuous function , we partition the closed interval

into

subintervals, as shown in the figure below.
 is an arbitrary point in 
, 
the subinterval of the partition.



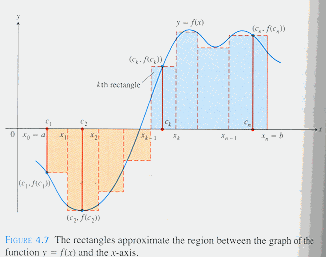
The area of a rectangle is length times width.
For a representative rectangle, the width is

and the length, or height, is
,
so its area is
.
The expression
,
called a Riemann sum,
gives the sum of the areas of all the rectangles shown in the figure.
This sum gives an approximation of the algebraic area under the graph of

bounded by the x-axis and the vertical lines  and  .

Now take the limit:

If we simultaneously let the number of subintervals increase beyond all bounds
- go to infinity -
and the length of each subinterval go to zero, and if this limit exists,
that is, is a finite number, this limit is called the definite integral of
over .

,
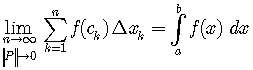where   is the norm of the subintervals,
that is, the maximum value of the lengths of the subintervals.

Example
1] Find the area of the region between the parabola
and the x-axis on the interval
.

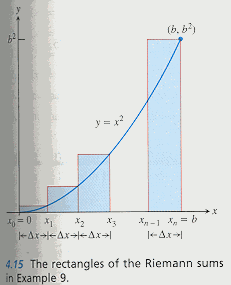tiff
Partition

into n subintervals each of length
.
The points of partition are
.
The choice of the

in the subinterval

is arbitary , choice a point that makes the algebra as easy as possible.
Let

be the endpoints of each subinterval.
.
So the areas of the corresponding rectangles are:


is the area of the first rectangle.


is the area of the second rectangle.
.
.
.

is the area of the  rectangle
.
.
.

is the area of the last, or   rectangle.
The sum of these areas approximates the precise value of the area under the curve.

.

can be moved across the summation sign because it does not involve
the summation index  .
With respect to the summation, is a constant.
At this point, we need to use the summation formula

.
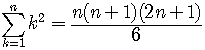Remember that
.
So


      

      .

To get the exact value of the area under the curve, we let the number of subintervals
go to infinity,
,
and the maximum length (the norm) of the subintervals go to ,
.
This value is the value of the definite integral.



                 

2] For a particular vale of   , say , we can interpret the result

as giving the area under the graph of
 from    to  ,
or simply as the value of the definite integral.

See Example 3, page 345.


Another application of the definite integrals to define the
Average (Mean) Value of a Function
If the integral of a function exists on
, then the average (mean) value of the function on is given by
.

Example
3]
The average value of   on  is



When we study the Fundamental Theorem of Calculus in the next section,
we will learn a relatively easier way of calculating this definite integral.
For now, we can find it using the definition of a definite integral as the limit
of a Riemann sum. But that would require a bit of algebra!
Here's an easier way:
The graph of

is the upper semicircle of radius  .
The geometric interpretaion of the definite integral is as the area of the
semicircle from
  to .
From plane geometry, the area of this semicircle is
.
So
.


Rules for Definite Integrals
1] Order of Integration:


2] Zero:


3] Constant Multiple:


4] Sum and Difference:


5] Additivity:


6] Max-Min Inequality:
If    and   are the maximum and minimum values of
 on , then
.

7] Domination:
If on   ,  then
.
In particular, if ,   then   .

See Examples 5, page 348.


       next  The Mean Value and Fundamental Theorems
               Top