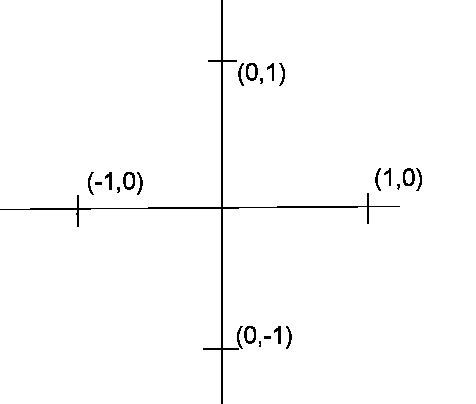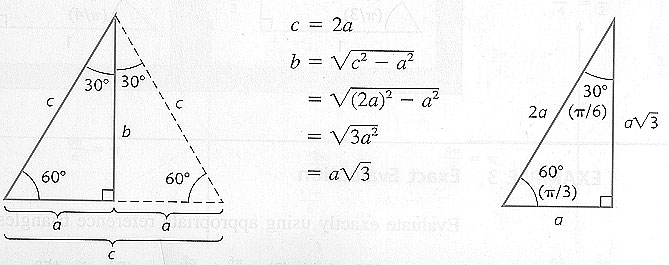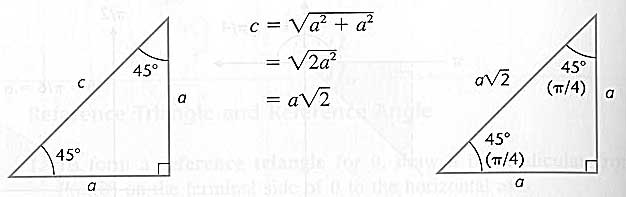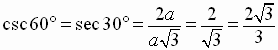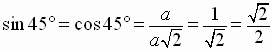Exact Values of the Trigonometric Functions for Special Angles

The trigonometric functions of most angles are irrational numbers,
so only approximate values are used when we perform calculations.
For example,
                  
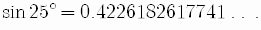
The exact value is a non-repeating infinite decimal.
When we calculate, we have to round-off, say to the sixth decimal place.
                
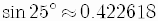
is an approximation of the true, exact value.

For some angles the trigonometric functions can be given an exact expression.

              Quadrantal Angles
are angles whose terminal sides lie along a coordinate axis.



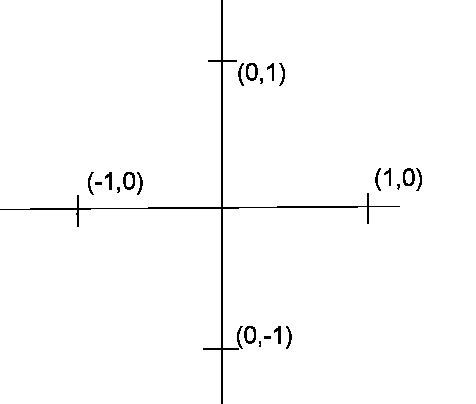
Remember the definition of the trigonometric functions as various ratios
involving the coordinates of a point, 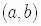,or the positive distance, ,
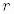of the point from the origin of the coordinate system.
For example,
                    

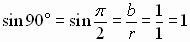
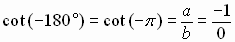         is not defined, because we can not divide by zero.

          See Example 1, page 445.



        Reference Triangles and Reference Angles


              
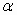                                         is always positive

1]
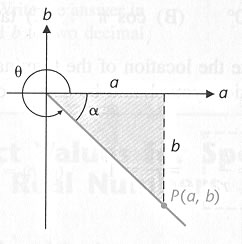
      To form a reference triangle for 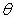, draw a perpendicular from a point
      on the terminal side of 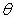to the horizontal axis.

2]
      The reference angle 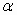is the acute angle (always taken positive) between the terminal side
      of 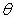and the horizontal axis.

The reference triangle and the reference angle enables us to calculate the trigonometric functions
of any angle, regardless of how big the angle is or whether it is positive or negative.

                See Example 2, pages 446 - 447, of the textbook.


              Evaluation for 30 - 45 - 60 Degree Angles

A 30-60 degree right triangle forms half an equilateral triangle.
All sides are equal in an equilateral triangle and we can apply
the Pythagorean Theorem to get a relationship among the three
sides of the original 30 - 60 degree right triangle.


            


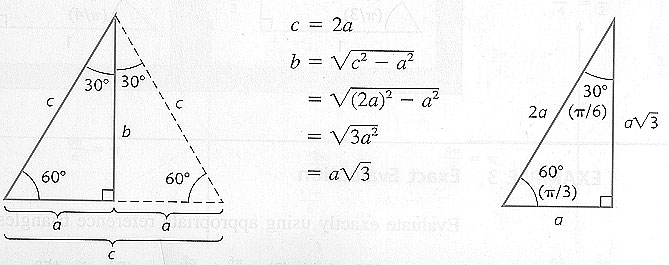
For a 45 degree right triangle the Pythagorean Theorem gives:



                  

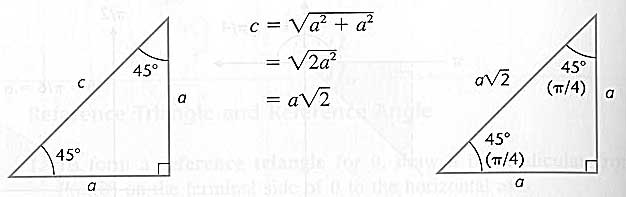
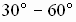We can easily find the exact value of the six trigonometric functions of these special angles.


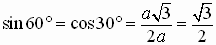
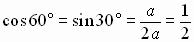
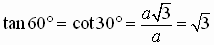
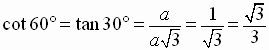
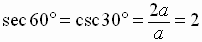
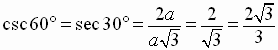
                            Angles

            

          


          

          

          

          



                      Angles

          

          

          

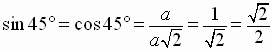
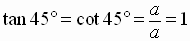
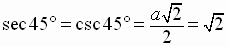
                    See Examples 3 – 5, pages 448 – 452, of the textbook.

                              top
                              next   Circular Functions