Sum,
Difference, and Cofunction Identities
Sum
and Difference Identities for the Cosine
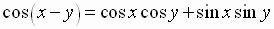

Cofunction
Identities
The cosine, cotangent, and cosecant functions are known as cofunctions
of the sine, tangent, and secant functions.
Using the first identities above,
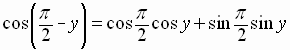
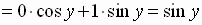
So we have the
cofunction
identity for the cosine
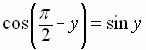
Letting  in this equation, we get
in this equation, we get
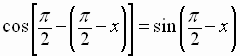
cofunction
identity for the sine
 .
.
Since
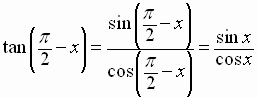
we get the
cofunction
identity for the tangent

These identities are true for any real number or any angle in radian measure.
If 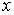 is
in degree measure,
is
in degree measure,
replace
 with
with 
Sum
and Difference Identities for Sine and Tangent
Using the cofunction identity for the cosine, we can write
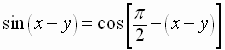
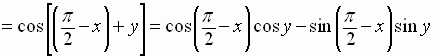 .
.
Simplifying, we get the
Difference
Identity for the Sine Function
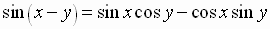
If we replace 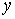 by
by 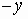 , we
get the
, we
get the
Sum
Identity for the Sine Function
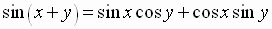
Since the tangent is the ratio of the sine to the cosine, simple algebra gives
the
Difference
Identity for the Tangent Function
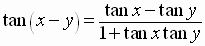
If we replace 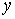 by
by 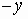 ,
we get the
,
we get the
Sum
Identity for the Tangent Function
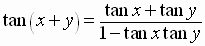
See Examples 1 – 5, pages 537 – 540, of the textbook.
top
next Double-Angle
and Half-Angle Identities
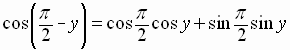
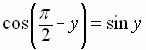
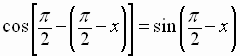
 .
.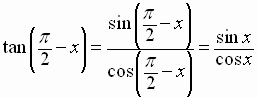

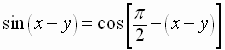
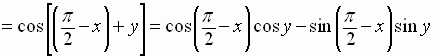 .
.