Trigonometric Equations

Previously, the equations we studied are identities
These are equations that are true for all valid replacements of the variable(s)
for which both sides of the equations are valid
Now we consider conditional equations,
which may be true for some replacements of the variable
but false for other replacements of the variable

For example,
                         
is a conditional equation, because it is true for ,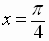
but false for other values of the variable, for example, it is is false for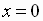

We will look at two ways of solving conditional equations:
1] solving the equation algebraically, which may lead to exact solutions of the equation
2] solving the equation graphically, which usually do not give exact solutions,
     only approximate solutions of the equation


                         The Algebraic Way

Exact solutions using factoring – see Example 1, pages 558 - 559, of the textbook

Approximate solutions using identities and factoring – see Example 2, pages 559 – 560, of the textbook

Approximate solution using substitution – see Example 3, pages 560 – 561, of the textbook

Exact solutions using identities and factoring – see Example 4, pages 561 - 562, of the textbook

Approximate solutions using the quadratic formula – see Example 5, pages 562 - 563, of the textbook


                        The Graphic Way

Solution using a graphing utility - – see Examples 6 - 9, pages 563 - 566, of the textbook


                           top             
                          next   Law of Sines
                                     begin Module 3
                                    Additional Topics in Trigonometry