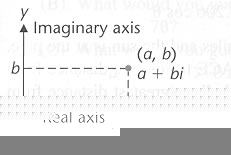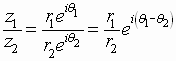Complex Numbers in Rectangular and Polar Forms
The rectangular form of a complex number is
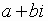 where
where 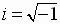
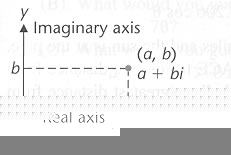
Complex
Plane
The point 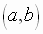 can be
associated with the complex number
can be
associated with the complex number 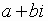
See Example 1, page 628, of the textbook
Polar
Form
Using the conversion equations
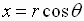
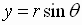
the complex number
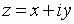
can be written in polar form
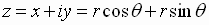
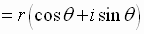
This
conversion is shown in the graph

FIGURE
1
In the calculus the famous relation
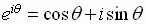
is proved
Then the polar form of a complex number also can be written as
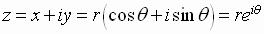
Note that if we let 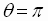 ,
we get
,
we get
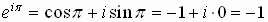
or
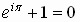
an amazing equation relating these five very important numbers!
Since the sine and the cosine functions are periodic functions with period 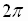 ,
,
we can write
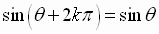
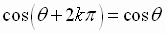
for
any integer 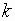
Then we can write the
General Polar Form
Of A Complex Number
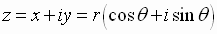
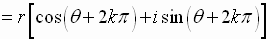
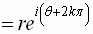
for
any integer 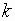
The number 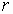 is called the modulus, or absolute value, of
is called the modulus, or absolute value, of 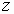 and is denoted
and is denoted
by mod 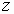 or
or 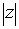
The polar angle 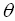 that the line joining
that the line joining 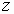 to
the origin makes with the polar axis is called
to
the origin makes with the polar axis is called
the argument of 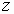 and is denoted by arg
and is denoted by arg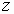
From Figure 1 we see that
Modulus
and Argument for 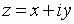
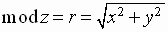 This quantity is never negative
This quantity is never negative
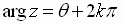 for any integer
for any integer 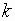
where
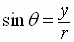 and
and
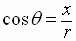
The argument 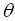 is conventionally chosen so that
is conventionally chosen so that
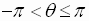 (radians)
(radians)
or
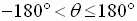 (degrees)
(degrees)
Conversion Rectangular to Polar Form –
See
Example 2, pages 630 - 631, of the textbook
Polar
to Rectangular Form –
See
Example 3, pages 631 - 632, of the textbook
Multiplication
and Division in Polar Form
If
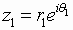 and
and 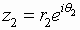 ,
then
,
then
1]
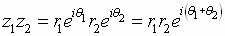
2]
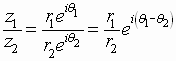
See Example 4, page 633, of the textbook
top
next De
Moivre's Theorem