Geometric
Vectors
Quantities that can be specified by a single number are called scalar quantities.
Examples are weight, area, length, volume
Quantities that require two things to be specified, namely, magnitude and direction,
in order to be uniquely determined are called vector quantities
Examples are forces, velocities, directed distances
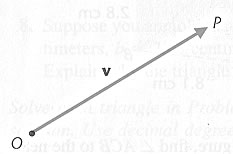
The
vector 
O is called the initial point
P is called the terminal point
The magnitude of the vector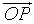 ,
,
denoted
by  or
or 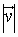 ,
,
is the length of the directed line segment from O to P
The direction of the vector, as given in the figure above, is the direction
from O to P
This direction may be quantified in terms of the angle that the directed line
segment 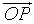
makes with a horizontal axis, for example, the x-axis of a Cartesian coordinate
system
Two vectors have the direction if they are parallel and point in the same direction
Two vectors have opposite direction if they are parallel and point in opposite
directions
The zero vector ,
denoted
by 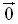 ,
,
has a magnitude of zero and an arbitrary direction
Two vectors are equal if they they have the same direction and magnitude
The sum of two vectors 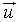 and
and
 can be defined in
two equivalent ways:
can be defined in
two equivalent ways:
1]
Using the tail-to-tip
rule:
Translate
 so that its tail
end (initial point) is at the tip end (terminal point)
of
so that its tail
end (initial point) is at the tip end (terminal point)
of 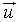
Then,
the vector from the tail end of 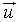 to the tip end of
to the tip end of  ,
is the sum , denoted by
,
is the sum , denoted by
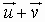 ,
of the vectors
,
of the vectors 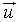 and
and

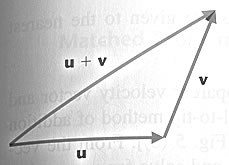
2]
Using the parallelogram rule:
The sum of two nonparallel
vectors 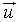 and
and  is the diagonal of the parallelogram formed using
is the diagonal of the parallelogram formed using
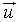 and
and  as adjacent
sides
as adjacent
sides

If 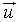 and
and  are parallel,
use the tail-to-tip rule
are parallel,
use the tail-to-tip rule
The vector 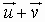 is also
called the resultant of the two vectors
is also
called the resultant of the two vectors 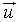 and
and 
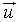 and
and  are called the vector components of
are called the vector components of 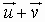
In particular, vectors can be resolved into rectangular components
Note that , like real numbers, vector addition is
commutative

and
associative

Problems involving vectors often reduce to the problem of solving triangles,
so trigonometry navigates to the rescue
See Examples 1- 3, pages 597 – 601, of the
textbook
top
next Algebraic
Vectors


