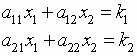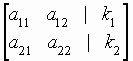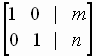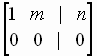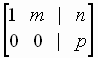Gauss-Jordan
Elimination
We will look at systems of equation with more than two variables
We will not require that a system have the same number of equations as variables
Possible Solutions to a System of Linear Equations
Any system of linear equations has exactly
one solution
no solution
or
an infinite number of solutions
regardless of the number of equations or the number of variables in the system
The terms unique, inconsistent, dependent, and independent
are used to describe the solutions of any system of linear equations
In the previous section (systems of linear equations and augmented matrices)
row operations
were used to transform the augmented matrix of a system of two equations in two
variables
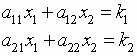
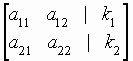
into one of the simplified forms
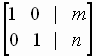
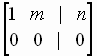
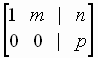
Form 1
Form 2
Form 3
where 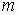 ,
, 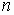 ,
and
,
and 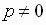 are real numbers
are real numbers
Each of these reduced forms represents a system
that has a different type of solution set, and no two of these forms are row-equivalent
We consider each of these forms to be a different simplified form
Now we will look at larger systems with more equations and more variables
Definition of Reduced Matrix
A matrix is in reduced form if
1] Each row consisting entirely of 0’s
is below any row having at least one nonzero element
2] The leftmost nonzero element in each
row is 1
3] The column containing the leftmost
1 of a given row has 0’s above and below the 1
4] The leftmost 1 in any row is to the
right of the leftmost 1 in the preceding row
See Example 1, pages 677 – 678, of the
textbook
Solving Systems of Linear equations by Gauss-Jordan Elimination
The method transforms an augmented matrix into a reduced form
The system corresponding to a reduced augmented coefficient matrix
is called a reduced system
See Example 1, pages 677 - 678, of the textbook
Gauss-Jordan Elimination
Step 1.
Choose
the leftmost nonzero column and use appropriate row operations
to
get a 1 at the top
Step 2.
Use
multiples of the row containing the 1 from Step 1 to get zeros
in
all remaining places in the column containing this 1
Step 3.
Repeat
Step 1 with the submatrix formed (mentally) by deleting the row
used
in Step 2 and all rows above this row
Step 4.
Repeat
Step 2 with the entire matrix, including the mentally deleted rows.
Continue
this process until it is impossible to go further
Notes:
1] Although each matrix has a unique reduced form, the sequence
of steps given here
for transforming a matrix into a reduced form
is not unique
Other sequences of steps (using row operations)
can produce a reduced matrix
2] If at any point in the process we get a row with all zeros to the
left of the vertical line
of the augmented matrix and a nonzero number
to the right of the vertical line, we must
stop, since we have a contradiction
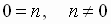
Conclude that the system of linear equations
has no solution
3] If the number of leftmost 1’s in a reduced augmented matrix
is less than the number
of variables in the system and there are no
contradictions, then the system is dependent
and has infinitely many solutions
Solve each equation in a reduced system for
its leftmost variable and then introduce
a different parameter for each remaining variable.
This method gives concise representation of
the solutions of a dependent system
of linear equations
See Examples 2 – 6, pages 679 –
686, of the textbook
top
next
Systems Involving Second-Degree Equations