Systems of Linear Equations and Augmented Matrices

In a system of two linear equations in two variables
          
          
where x and y are the variables,
the quantities a, b, c, and d are real numbers called the coefficients of x and y
and
the quantities h and k are real numbers called the constant terms of the system
An ordered pair (x₀,y₀) is called solution of the system if each equation
in the system of equation is satisfied by the pair
The set of all such ordered pairs of numbers is called the solution set of the system

Two methods of solving this system of two equation equations in two variables are
     the method of substitution
                        and
     the method of elimination-by-addition

We will introduce
                                   augmented matrices
to generalize the method of elimination-by-addition
to the solution of systems involving many linear equations and many variables.


     Solving a System by Graphing
See Examples 1 – 2, pages 659 – 660, of the textbook.

Basic Terms
A system of linear equations is consistent if it has one or more solutions
                                                        inconsistent if it has no solution

A consistent system is said to be independent if it has exactly one solution
                                                            dependent if it has more than one solution


Possible Solutions of a Linear System of Equations
The system
          
          
must have
     1]      Exactly one solution.
               In other words, the system is consistent and independent
OR
     2]      No solution.
              In other words, the system is inconsistent
OR
     3]      Infinitely many solutions
              In other words, the system is consistent and dependent

                    There are no other possibilities

See Example 3, page 662, of the textbook


Elimination by Addition
This method generalizes to higher-order systems
The method involves the replacement of systems of equations
with simpler equivalent systems of equations
Equivalent systems of equations are systems that have exactly the same solution set

               Operations Producing Equivalent Systems
A system of linear equations is transformed into an equivalent system if
     1]  Two equations are interchanged
     2]  An equation is multiplied by a nonzero constant
     3]  A constant multiple of another equation is added to a given equation

See Examples 4 – 5, pages 663 – 666, of the textbook


                         Matrices
A matrix is a rectangular array of numbers written within brackets
For example,

     

Each number in a matrix is called an element of the matrix
If a matrix has m rows and n columns, it is called an m x n matrix
The expression m x n is called the size of the matrix
The numbers m and n are called the dimensions of the matrix
The number of rows is always given first
A matrix with n rows and n columns is called a square matrix of order n
A matrix with only one column is called a column matrix
A matrix with only one row is called a row matrix

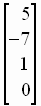                   is a 4 x 1 column matrix


                   is a 1 x 4 row matrix

The position of an element in a matrix is the row and column containing the element
Double subscript notation:
an element is denoted by
                                                       
where 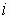is the row the element is in
where is the column the element is in.
For example, in the matrix above
     
     


The principal diagonal of a matrix consists of the elements
     
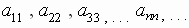
In other words, the elements in the matrix starting with the element in the upper left-hand corner
of the matrix and going down along the diagonal ending with the element in the lower right-hand
corner of the matrix


The augmented matrix of a system of linear equations in variables

     

     

     
                                            . . . . . . .
                                            . . . . . . .
                                            . . . . . . .
     


                                             is


     

The augmented matrix will be used in solving the system of linear equations


Remember, two systems of equations are said to be equivalent if they have the same solution
By definitions, two augmented matrices are said to be row-equivalent
denoted by the symbol
                                                  
between two matrices
if they are augmented matrices of equivalent systems of equations

The following theorem shows us how to transform augmented matrices into row-equivalent matrices
The theorem is used in the process of solving systems of linear equations



     Elementary Row Operations Producing Row-Equivalent Matrices

An augmented matrix is transformed into a row-equivalent matrix
if any of the following row operations is performed:

     1]  Two rows are interchanged 
     2]  A row is multiplied by a nonzero constant 
     3]  A constant multiple of one row is added to another row 
                    Notation: The arrow    means "replaces"



Solving Systems of Linear Equations Using Augmented Matrices
Notes:
1]  In general, if at the end of the process there is a row of 0's in an augmented matrix
     for a system of two equations in two variables, then the system of equations is dependent
     and there are infinitely many solutions

2]  If in a row of an augmented matrix there there are all 0's to the left of the vertical bar
     and a nonzero number to the right of the bar, then the system of equations is inconsistent
     and there are are no solutions


          See Examples 6 – 9, pages 668 – 673, of the textbook


                    top
                    next  Gauss-Jorden Elimination