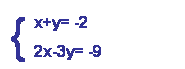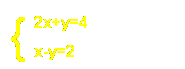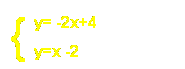Why should I care: This method can be used to help you out in many reallife situations. An example of this would be in multiple investments.

Using graphing to solve linear systems is a stellar method because it allows you to see what the linear system means, and what the solution is in a more understandable way.

Back Track: A linear system is formed by placing two equations together. After solving the system in two variables you should recieve an ordered pair that works in both equations. An ordered pair is a point on a graph, in this case the point where the two lines of the equations intersect.

Be prepared, learn to check a solution algebraically:

1) You substitute the x and y values of the ordered pair solution into the original system.

2) Solve each equation of the system, if the given answer to both equations matches the one you get when subsitituting the ordered pair into the system, then the solution is correct.

Ex) (3/2, 2)

(they are both true)

Yes, this ordered pair works, the solution is correct!!!

Steps to using the Graphing Method:

1. Translate each equation into slope-intercept form, so that both lines are easy to graph.

2. Graph both of the lines.

3. Find the point at which both lines intersect.

4. Check your solution in both of the original equations by means of substituting your x and y values of the intersection point in for the x and y in both of the original equations. (Use the method in Be Prepared)

Examples Using the Graphing Method:

ExA)

Graph:

The two lines intersect at (-3, 1), so that is the solution!!!

ExB)

Graph:

The two lines intersect at (2,0), so that is the solution!!!