Section 4.2: Multiplying Matrices



Matrix addition is easy as pie (3.14 haha) to learn!!!

You simply add together the corresponding numbers 
within the matrices together.  For instance, for 
the following 2 matrices, you would add the numbers 
8 and 10 together to get 18, and then add 3 and 3 
beside them to get 6.  When you add matrices, you 
are solving for one matrix.

	=



You can multiply to matrices together if the number of columns
 in one is equivalent to the number or rows in the other.
  ex.  a 4 by 2 matrix and a 2 by 3 matrix.  The end product will
 yield one matrix that has a row number of  4 and a column number 
of 3.  Since you had to have a column and row number being the same 
think of it this way: ( a 4 by 2 matrix meets a 2 by 3 matrix,
 = 4 x 2 2 x 4.  If you imagine the 2's running away to getr married,
 they would leave the 4 and 3 alone to create their own matrix.)  
Multiplying the matrices will seem tricky at first, but once you 
get the hang of it, it becomes simple.





You Try:
1)	4 x 6 * 6 x 3 =?
2)	3 x 4 * 4 x 7 =?
3)	15 x 23 * 15 x 24 =?

Answers:
1)	4 x 3
2)	3 x 7
3)	not possible. There isn't a row that is equal to the column.   





Multiplying Matrices


Matrices can be multiplied together to get a new set of numbers. 
(a different matrix)  Using the rule above (that only matrices with 
a like number of rows to columns can be multiplied together) we can 
multiply matrices.  To find the entry in the first row and first column 
of AB, multiply corresponding entries in the first row of A and the 
first column of B.  Then add

(-1)(-3) + (3)(-4) = -9


	


  = 


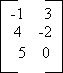
By continuing this pattern, you can obtain the following:


   = 


You Try:

1)  
	



Answers:

1)



This situation would be useful in real life if say, you need to 
multiply 2 sets of numbers together, and find equivalent numbers for each.