| Matriz de
propagación  Consideremos un rayo que se propaga en
línea recta desde el punto 1 hasta el punto 2, se
observa que q en 1 es igual a q en 2 es decir q1=q2 (igual dirección). La
pendiente de la recta es tan(q)=(y2-y1)/Dx, de donde y2=y1+Dx.tan(q), y de nuevo invocando la
aproximación paraxial tan(q)~sin(q)~q, resulta: y2=y1+Dx.q1; q2=0+q1 Consideremos un rayo que se propaga en
línea recta desde el punto 1 hasta el punto 2, se
observa que q en 1 es igual a q en 2 es decir q1=q2 (igual dirección). La
pendiente de la recta es tan(q)=(y2-y1)/Dx, de donde y2=y1+Dx.tan(q), y de nuevo invocando la
aproximación paraxial tan(q)~sin(q)~q, resulta: y2=y1+Dx.q1; q2=0+q1
A partir de estas
ecuaciones escribimos la respectiva ecuación matricial
 En este caso al aplicar la Transformación de
Propagación
al vector (y1,q1) resulta el vector (y2,q2) con la particularidad de
que la dirección no cambia (q1=q2). En este caso al aplicar la Transformación de
Propagación
al vector (y1,q1) resulta el vector (y2,q2) con la particularidad de
que la dirección no cambia (q1=q2).
Al
ampliar la matriz de propagación para incluir el
desplazamiento dx tenemos:
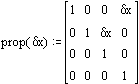 
 Atrás Atrás Adelante Adelante
A
la página Principal
|