Circunferencia
| RESEÑA HISTORICA | |
| GEOMETRIA | |
| CONCEPTOS | |
| BIBLIOGRAFIA | |
| CREDITOS |

|
CONCEPTOS BASICOS
La circunferencia es una línea curva cerrada, cuyos puntos tienen la propiedad de equidistar de otro punto llamado centro. El término equidistar significa que están a la misma distancia.
La circunferencia también divide al plano en 3 subconjuntos:
| Región interior, que recibe el nombre de círculo y a la que pertenece el punto centro. | |
| Frontera, que es la circunferencia misma. | |
| Región exterior, que queda afuera de ella. |
La circunferencia unida al círculo forma la región circular.

Para dibujar una circunferencia utilizamos el compás. Apoyamos la punta metálica en el punto que nos servirá de centro y luego trazamos la circunferencia. En caso de circunferencias muy grandes, por ejemplo, una circunferencia en el suelo, basta con colocar una estaca en el punto centro y desde allí, con una cuerda tensa y algo para marcar en su extremo, giramos para que se complete.
Elementos
Los principales elementos de una circunferencia son:
| Radio (r): es el segmento que une el punto centro con cualquier punto de la circunferencia. El radio permite nombrar a la circunferencia. Para ello, se coloca el símbolo de circunferencia, y luego, dentro de un paréntesis redondo, colocamos la letra del punto centro, una coma y después el nombre del segmento que forma el radio. Si no tiene letras, lo identificamos con r. |
Observa:

| Flecha: es el segmento de recta perpendicular a la cuerda en su punto medio, y que corta al arco. |
| Diámetro (d): es el segmento que une 2 puntos de la circunferencia, pasando por el punto centro. El diámetro equivale a la medida de 2 radios. |
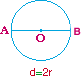
En nuestro ejemplo
el diámetro es AB
| Cuerda: es el segmento de recta que une dos puntos cualesquiera de la circunferencia sin tocar su centro. Te presentamos la cuerda |
___
MP :
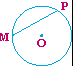
| Arco: es una parte o subconjunto de la circunferencia, limitada por 2 puntos de ella. Tiene símbolo propio. |
Por ejemplo: Arco FT.

Posiciones relativas de una recta y una circunferencia
Con respecto a una circunferencia, una recta puede tener 3 posiciones:
| Una recta y una circunferencia son disjuntas. Es decir, no tienen punto de intersección. |

| La recta es tangente a la circunferencia. En este caso, la recta toca a la circunferencia en un punto. Este punto recibe el nombre de punto de tangencia. Si dibujamos el radio que une el centro con el punto de tangencia, siempre obtendremos un trazo perpendicular a la recta. |

| La recta es secante a la circunferencia. Esto quiere decir que la intersecta en 2 puntos y una parte de ella es cuerda de la circunferencia. |

Relación entre polígonos y circunferencia
Los polígonos y la circunferencia se relacionan de acuerdo a la posición que ocupan los primeros con respecto a la circunferencia. Es así como tenemos las siguientes situaciones:
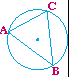
| Polígono inscrito a la circunferencia. En este caso los vértices del polígono son puntos de la circunferencia y ésta queda circunscrita al polígono. Los lados del polígono son cuerdas de la circunferencia. |
| Polígono circunscrito a la circunferencia. Todos los lados del polígono son tangentes de la circunferencia. La circunferencia queda inscrita al polígono. |
