CLASIFICACIÓN DE
GRAMÁTICAS
1.3 ESTRUCTURAS DE LAS GRAMÁTICAS
2.
CLASIFICACIÓN DE LAS GRAMÁTICAS
2.1 Tipo 0.- Gramáticas
Con Estructura De Frase
2.2 Tipo 1.- Gramáticas
Dependientes De Contexto
Ejemplo 2
Ejemplo 3
2.3 Tipo 2.- Gramáticas
Libres de Contexto
Ejemplo 4
Ejemplo 5
2.4 Tipo 3.- Gramáticas Regulares
2.5
Características De La Clasificación
GLOSARIO
REFERENCIAS
ÍNDICE FIGURAS
Fig. 1.
Los Cuatro Tipos De Gramáticas
Según Chomsky
CLASIFICACIÓN DE GRAMÁTICAS
I. NOCIÓN DE GRAMÁTICA
1.1 DEFINICIONES BÁSICAS
Empecemos por definir que es un lenguaje, pero para esto
tenemos que definir alfabeto.
Alfabeto el
conjunto no vacío y finito de símbolos, dichos símbolos tienen una secuencia de
longitud finita, cada secuencia se conoce como palabra o cadena, este
último término se da para evitar la idea de identificar el término palabra con
las palabras de algún lenguaje natural.
La cadena vacía, la cual se denota por el
símbolo ε(epsilon) , es una palabra sobre cualquier alfabeto y se
define como una secuencia vacía de símbolos tomados de cualquiera que sea el
alfabeto en cuestión.
Un lenguaje es un conjunto de cadenas, es decir está
compuesto por un alfabeto.
Los
lenguajes pueden ser bastantes grandes, por ejemplo el lenguaje {1, 11, 111,
1111, 11111, ...} formado por todas las cadenas finitas de unos. Obsérvese que
este lenguaje es infinito (aunque cada cadena del mismo tenga la longitud
finita). Cuando un lenguaje tiene un tamaño muy grande es difícil especificar
que cadenas le pertenecen.
1.2 OPERACIONES CON CADENAS
Si w es una cadenas sobre cualquier alfabeto, su longitud se denota mediante el
símbolo | w | y se define como el número de símbolos que tiene la cadenas.
Si w y z
son cadenas, la concatenación de w con z es la cadena que se obtiene al añadir
a la cadena w la palabra z, y se denota wz o w . z. Obsérvese que se tiene que:
|
wz | = | w | + | z |
La
concatenación de la cadena vacía ε con cualquier otra cadena w, no
modifica a la palabra w. Por esta razón, ε se comporta como identidad con respecto
a la operación de concatenación.
La
potencia de una cadena sobre un alfabeto se define como sigue:
Sea w una
cadena; para n Є N se define
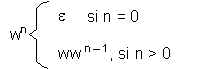
Se dice
que wi es la potencia i-ésima de w.
Si w y z son cadenas, se dice que w es igual a z, si tienen la misma longitud y los mismos símbolos en la misma posición. Se denota mediante w=z.
Si w
y x son cadenas, se dice que x es prefijo de w, si
para alguna cadena y se obtiene w = xy. Si se considera y =
ε, entonces para w = xy se tiene que w = x, con lo
que toda palabra puede considerarse prefijo de sí misma. La cadena vacía ε
es prefijo de cualquier palabra.
Una cadena
w es una subcadena de otra cadena z si
existen la cadenas x e y para las cuales, z = xwy.
La inversa
o transpuesta de una palabra w, es la imagen refleja de w. Para denotar la
inversa de w se usa wç.
Una definición más precisa de la misma puede ser la siguiente:
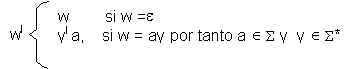
La inversa se "deshace" a sí misma. Es decir, ((x) ç )ç= x.
1.3 ESTRUCTURAS DE LAS GRAMÁTICAS
El sistema
de estructuración de frases (secuencias arbitrarias finitas de símbolos)
expresadas correctamente, es decir, si es una frase significativa, se define
como gramática.
La
gramática consiste en dos conjuntos finitos, uno de
símbolos no terminales y otro de símbolos terminales, un subconjunto finito de
producciones y de un símbolo inicial. Su representación es:
(N, T, P, S)
donde:
N. Símbolos No Terminales.
Son los símbolos introducidos para la definición de la gramática y que no
figuran en las sentencias del lenguaje, deben ser definidos por otras
producciones (o reglas BNF); es decir, también aparecen en el lado izquierdo de
las producciones. Los símbolos no terminales son variables sintácticas y se
conocen No-terminales.
T. Símbolos Terminales.
Son los símbolos que realmente aparecen en una frase. Nunca aparecerán en el
lado izquierdo de una producción. Los símbolos terminales deben ser símbolos
válidos del lenguaje. Sus elementos se denominan Terminales. Generan una única
cadena, ella misma.
N Ç T =Φ
T* representa el conjunto de todas las cadenas
posibles en T.
P. Conjunto de Reglas de
derivación. Son las reglas para la sustitución de cadenas y se denominan
producciones Se definen por medio de un par ordenado, escritos sus elementos
entre paréntesis y separados con una coma, o pueden estar por medio de la
notación BNF (Backus Normal Form), teniendo una parte izquierda y una parte
derecha separadas por una flecha, la cual se lee como: Se define como.
a à
b
Imponiendo
restricciones a las posibles formas de las producciones se obtienen distintos
tipos de gramáticas. Por ejemplo:
Restricciones respecto a que pueden ser a y b .
Restricciones de dónde se puede aplicar la
transformación establecida por la producción.
S. Es el símbolo no-terminal mas
importante del conjunto N, se le llama Símbolo
inicial. Genera todas las cadenas del
lenguaje.
La
gramática G1 define todas las tiras formadas por varias aes seguidas de igual número de bes
(que en la descripción algebraica sería: anbn), y su
cuarteto quedaría de la siguiente manera:
G1
= (S, ab, P, S)
Donde P
es:
Sà
ab
Sà
aSb
R
Para decir que una cadena está dentro de una
gramática debemos tener elementos terminales.
R
El estado inicial en las reglas de producción
es cero y produce una letra y además deja espacio para seguir produciendo.
R
Si se va a repetir una letra o dígito se hace
un ciclo.
R
Una gramática puede tener varias producciones
y la forma de terminar el análisis es cuando la cadena contenga elementos
terminales.
R
Los conjuntos de elementos terminales y no
terminales son disjuntos.
R
Todas las producciones deberán contener, al
menos, un elemento no terminal en su lado izquierdo.
II. CLASIFICACIÓN DE LAS GRAMÁTICAS
Esta
clasificación fue publicada por Noam Chomsky en el año 1959; introdujo entonces
cuatro tipos de gramáticas a base de cambiar sólo el tipo de las reglas de
derivación (las restricciones).
2.1
TIPO 0.- GRAMÁTICAS CON ESTRUCTURA DE FRASE
No hay
restricción en las producciones, es decir, P tiene la forma mas general:
a à b
donde:
a Є (N È T)+
b Є (N È T)*
Es decir, que
la parte izquierda de una regla pude ser una cadena de símbolos cualesquiera de
N y T, y la parte derecha lo mismo y además puede ser nula.
2.2
TIPO 1.- GRAMÁTICAS DEPENDIENTES DE CONTEXTO
En ella
la forma de la regla de P es la siguiente:
a A bà
a
g
b
donde:
a, b
Є (N È
T)*
A Є
N
g Є
(N È
T)+ , es decir g debe ser
no vacío.
La
producción no se aplica siempre, sino en determinados contextos: solo se cambia
A por gamma, pero sólo en el contexto formado por alfa...beta.
Validar la cadena w = aabbcc con la
gramática de contexto sensitivo:
G2= í
(a,b,c) , (B,C), P , Sý
P:
S à
aSBC|abC
CB à BC
bB à bb
bC à bc
cB à Bc
cC à cc
Se toma del estado inicial aSBC, y se van
derivando los elementos según las producciones, hasta obtener la cadena w:
Sà
aSBC
à
aabCBC
à
aabcBC
à
aabBCC
à
aabbcC
à
aabbcc La
cadena es válida.
Validar la
cadena w = xyxyxyyy
G3= í
(x,y,z) , (X,Y,Z ), P , Sý
P:
S à xyXY|xxZ|yyZ
X à xY|xX
xX à
xx
Y
à
yX|yY
yY à
yy
Z à
xyZ|xy|yx|yyY
xZ à
xz
yZ à
yz
Obteniendo
la cadena w:
Sà
xyXY
à xyxYY
à xyxyXY
à xyxyxYY
à xyxyxyYY
à xyxyxyY
à xyxyxyyY
à xyxyxyyy La cadena es válida
2.3
TIPO 2.- GRAMÁTICAS DE LIBRE CONTEXTO (GLC)
La forma
de P es ahora:
A à a
donde:
A Є
N y siendo el único no terminal.
a Є
(N È
T)*
Es
decir, el conjunto P es un subconjunto del producto cartesiano N x (N È T)*
La denominación
de contexto libre es porque se puede cambiar A por a,
independientemente del contexto en el que aparezca A.
G4= í (a,+,*,(,) ) , (T,F), P , Eý
P:
E à E + T
E à T
T à T * F
T à F
F à (E)
F à a
Validar la cadena w= (a+a)*(a+a)
Eà T
à T*F
à T*(E)
à T*(E+T)
à T*(T+T)
à T*(F+F)
à T*(a+a)
à F*(a+a)
à (E)*(a+a)
à (E+T)*(a+a)
à
(T+T)*(a+a)
à
(F+T)*(a+a)
à (a+T)*(a+a)
à (a+F)*(a+a)
à (a+a)*(a+a) La
cadena es válida
G5= í (a,+,-,*,/,(,) ) , (T,F), P, Eý
P:
E à E + T | E – T
E à T
T à T * F | T / F
T à F
F à (E)
F à a
Validar la cadena w= ( (a+a)-(a-a) ) * a/a
Eà T
à T/F
à
T*F/F
à T*F/a
à T*a/a
à F*a/a
à (E)*a/a
à (E-T)*a/a
à
(T-F)*a/a
à (F-F)*a/a
à ((E)-(E))*a/a
à ((E+T)-(E-T))*a/a
à
((T+F)-(T-F))*a/a
à
((F+a)-(F-a))*a/a
à ((a+a)-(a-a))*a/a La cadena es válida
2.4 TIPO 3.- GRAMÁTICAS REGULARES
Las
reglas de P son ahora de una de las dos formas:
A à aB
A à a
donde:
A,B
Є N
A Є
T
Las
gramáticas regulares están muy relacionadas con la teoría de autómatas, puesto
que el autómata de estados finitos es capaz de reconocer o analizar las cadenas
de un lenguaje regular.
A estas
gramáticas se les llama regulares por la izquierda.
2.5 CARACTERÍSTICAS DE LA CLASIFICACIÓN
R
Cada gramática de un tipo es también del tipo
anterior (Fig. 1).
R
Cada una de ellas es mas restringida que la
anterior, es decir, comprende un menor número de lenguajes.
R
Cuanto menos restrictiva es una gramática, mas
complejo es su análisis sintáctico.
R
Las mas sencillas son las de Tipo 3.

Fig. 1.- Los cuatro
tipos de Gramáticas según Chomsky
GLOSARIO
Alfabeto o Vocabulario. Conjunto de todos los símbolos que
forman las sentencias del lenguaje.
Cadena. Secuencia ordenada de los símbolos que forman un
lenguaje.
Gramática. Estructuración de cadenas expresadas correctamente.
Lenguaje. Conjunto de cadenas.
Símbolo. Es un componente elemental del vocabulario del lenguaje
que se emplea para formar cadenas del lenguaje.
REFERENCIAS
Internet:
http://www.cps.unizar.es/~ezpeleta/COMPI/4/sld016.htm
Bibliografía:
SANCHIS, Llorca F. ; GALAN Pascual C. - COMPILADORES,
TEORÍA Y CONSTRUCCIÓN.- Ed. Paraninfo.

