{menu}

The Counting QuickPerm Algorithm (Head):
A Comparable Solution Inspired by Heap's Algorithm

The QuickPerm algorithm presented earlier utilized a countdown process, whereas this algorithm (below) will utilize a counting process. The significant difference between a countdown QuickPerm algorithm and a counting QuickPerm algorithm is the initialization of the primary controller array p[N]. A countdown process will initialize the controller array to corresponding index values, whereas a counting process will initialize all values in the controller array to zero. Whether a countdown process or a counting process is utilized is rather debatable. Both counting processes offer similar advantages and only a few minor disadvantages if any.

In any case scenario, the primary controller array p[N] within the QuickPerm algorithm(s) is analogous to an incremental base N odometer, where the least significant digit p[0] is zero, digit p[1] counts in base 2 (binary), digit p[2] counts in base 3, ..., and digit p[N-1] counts in base N. Initially the default upper index variable i is set to one as reference to the binary odometer digit which later advances by one each time a corresponding digit flips or rolls over. Since the upper index variable is clearly odd, the default lower index variable j is assigned to the odometer digit referenced by the upper index which coincides to the value stored in p[i] or zero. The first SWAP is executed on the target data structure(s) and the odometer digit/wheel referenced by the upper index advances...

Before another swap can take place, upper and lower index values must be recalculated based upon values stored in the base N odometer p[N]. Again the upper index begins at binary digit p[1] and attempts to flip each consecutive digit by adding one. The upper index will settle upon the first digit that will not flip. If the upper index is even, the lower index is assigned to the least significant odometer digit which coincides to the value stored in p[0] (or simply the lower index will remain at zero). Otherwise the lower index will be assigned to the actual odometer digit now referenced by the upper index. A second SWAP is executed on the target data structure(s) and the odometer digit/wheel referenced by the upper index advances.

This process continues until the upper index attempts to reference an odometer digit beyond the length of the linear permutable target in question.

Observable modifications compared to the countdown QuickPerm algorithm include the following:
  1. Initializing all integers in the controller array to zero.
  2. Increment p[i] by one after the conditional assignment j = p[i]
  3. While p[i] equals i DO reset p[i] to zero then increment i by one.
Also notice the nested while loop was replaced by a conditional if-else statement, which in-turn reduced the size of the index controller array by one integer. Although performance is relatively unchanged, using a nested while loop instead of a conditional if statement clearly lead to the development of a permutation class as presented in Example_05. This conditional substitution can be made regardless of the counting process utilized. Here's the counting QuickPerm C++ algorithm for your review:

A Counting QuickPerm Algorithm - Head Permutations Using a Linear Array without Recursion 

// NOTICE:  Copyright 2008, Phillip Paul Fuchs

#define N    12   // number of elements to permute.  Let N > 2

void QuickPerm(void) {
   unsigned int a[N], p[N];
   register unsigned int i, j, tmp; // Upper Index i; Lower Index j

   for(i = 0; i < N; i++) {  // initialize arrays; a[N] can be any type
      a[i] = i + 1;   // a[i] value is not revealed and can be arbitrary
      p[i] = 0;       // p[i] == i controls iteration and index boundaries for i
   }
   //display(a, 0, 0);   // remove comment to display array a[]
   i = 1;   // setup first swap points to be 1 and 0 respectively (i & j)
   while(i < N) {
      if (p[i] < i) {
         j = i % 2 * p[i];   // IF i is odd then j = p[i] otherwise j = 0
         tmp = a[j];         // swap(a[j], a[i])
         a[j] = a[i];
         a[i] = tmp;
         //display(a, j, i); // remove comment to display target array a[]
         p[i]++;             // increase index "weight" for i by one
         i = 1;              // reset index i to 1 (assumed)
      } else {               // otherwise p[i] == i
         p[i] = 0;           // reset p[i] to zero
         i++;                // set new index value for i (increase by one)
      } // if (p[i] < i)
   } // while(i < N)
} // QuickPerm()
QuickPerm - Function to Display Permutations (Optional) 

// NOTICE:  Copyright 2008, Phillip Paul Fuchs

void display(unsigned int *a, unsigned int j, unsigned int i) {
   for(unsigned int x = 0; x < N; x++)
      printf("%d ",a[x]);
   printf("   swapped(%d, %d)\n", j, i);
   //getch();  // Remove comment for "Press any key to continue" prompt.        
} // display()



Fundamental Analysis of QuickPerm Above
Number of Objects
to Permute (N)		 a[N] Display of
Initial Sequence		 a[N] Display of
Final Sequence		 Total Number of Unique
Combinations Produced (N!)
3 1 2 3 3 2 1 2 * 3 = 6
4 1 2 3 4 2 3 4 1 6 * 4 = 24
5 1 2 3 4 5 5 2 3 4 1 24 * 5 = 120
6 1 2 3 4 5 6 4 5 2 3 6 1 120 * 6 = 720
7 1 2 3 4 5 6 7 7 2 3 4 5 6 1 720 * 7 = 5040
8 1 2 3 4 5 6 7 8 6 7 2 3 4 5 8 1 5040 * 8 = 40320
9 1 2 3 4 5 6 7 8 9 9 2 3 4 5 6 7 8 1 40320 * 9 = 362880
if N is even 1 2 3 . . . (N - 1) N (N - 2) (N - 1) 2 3 4 . . . N 1 (N - 1)! * N = N!
if N is odd 1 2 3 . . . (N - 1) N N 2 3 . . . (N - 1) 1 (N - 1)! * N = N!


 A Permutation Ruler:
A Permutation Ruler

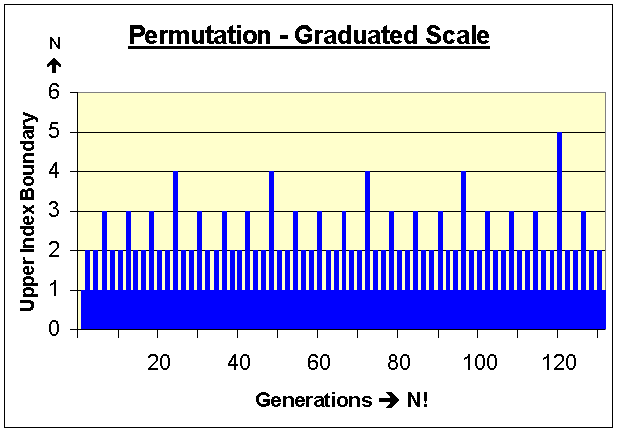
Next is tail combinations represented in EXAMPLE 02.

[New Book: Practical Permutations]

[QuickPerm] | [EXAMPLE 02] | [EXAMPLE 03] | [EXAMPLE 04] | [MetaPerm]
[Download the Five C++ Examples] | [Permutation Exercises]
[Contact the Author] | [Make a Donation] | [Links]
[HOME]

Help keep public education alive! We need your donations, click here to help now...

{top}

Copyright © 2008 by Phillip Paul Fuchs, all rights reserved.
Abstracting with credit is permitted...