


Genetic Programming Library Description
This is by far my most ambitious programming project to date. For all of those unfamiliar with the concepts of Genetic Programming I will give a brief description below, and then talk a little bit about how the program works.
Gentic Programming, What is it?
It is not Genetic Algorithms (GA). They are quite similar, and use the same basic principles, but there are some definite differences which I believe make Genetic Programming (GP), superior to GA's. Lets first discuss some of the basics, then the differences between GP's and GA's, and then I will talk about why GP's are better.
Genetic Programming Basics.
What's a Genetic Algorithm?
Advantages of GP's
Disadvantages fo GP's
Program Discription.
The idea behind Genetic Programming is to use the force of natural selection (Darwinism) to allow the computer to write its own programs. In nature, every living being is defined by its DNA. Their genes determine species, shape, size, color, and so on. In any enviorment there are certain individuals that have DNA which allows them to adapt better, and thus survive longer. Hopefully for them, they can survive long enough to reproduce and send their genes to future generations. Genetic programming is exactly the same, but with two big differences.
The first difference is that instead of evolution working on a population of DNA, it works on a population of Sexpressions. Sexpressions are modeled after tree structures and derive their name from the s-expressions used in lisp. The original forms of this type of programming were all done in lisp. Each Sexpression is made up of nodes which can be either terminal points or operation points. Terminal points can only be used as leaves of the tree, and they are some type of concrete thing like a number, variable, or action. Operation points are used everywhere else in the trree, and they are made of things like if statements, additions, divisions, or statements and so on. Lets say that you want to create a GP system that can match data to a specific curve (ie. Curve Fitting) even if you do not know what type of curve the data might represent. You would probably choose these elements as your operation nodes: +, -, /, *, Exp, Log, Sin, Cos. With those elements you should be able to match virtually any type of data you can find. You would then choose a constant and a variable for your Terminal nodes. This would define the types of nodes that are available for your system to use. The program would then make an initial population of Sexpressions by randomly picking available nodes to fill up the tree. So what you might end up with is something similar to Figure 1. That Sexpression is really the equation Y = ((X-2) + (Cos X) * X. Since you have a large population, typically about 500, of these equations you then just use natural selection to find the equation that most closely matches your data. At this point you might be wondering "What happens if you get X/0?" Division by zero will obviously cause an error. However, you can get around this problem by redifining the division operator to return 0 or NAN whenever someone attempts to divide by zero. The same thing can be done for ANY node that has potential problems. This means that any of the nodes are potentially interchangeable. In other words, you can change Y=X*0 with Y=X/0, and the result is still valid. The answer may be gibberish, but that is not important because all of the really unfit individuals will be killed.

Figure 1: This is a Sexpressoin
The second difference is that instead of nature determining fitness, you do. So in other words, the key to making your system perform is to determine the fitness criterion that will let your sexpression's evolve into the correct answer. If we go back to the previous example, then to determine fitness we would need to evaluate the Sexpression equation at various X values and compare the resulting Y value with the actual data. The more closely those values match the data, the fitter our Sexpressions are. The first generation is always very unfit because it was chosen at random. However, even within that first generation there are some individuals that are a slightly more fit than other individuals, and those are the ones that will reproduce. Reproduction in GP is typically done in two seperate parts. In the first part the first 10% of the next generation is made up of exact copies of members of the previous generation. Individuals that are to be copied are picked based on their fitness. This is called fitness proportionate reproduction. Basically it means that the higher fitness a Sexpression has, the more likely it is that it will be copied over into the next generation. It also means that occasionally even a very low fitness individual will be copied to the next generation. This ensures variety. The second part of the reproduction fills up the rest of the next generation and it is the operation of crossover. Crossover chooses two Sexpressions based on their fitness and randomly chooses a node in each one. It then swaps the subtrees where the chosen nodes are the root nodes of the two subtrees to swap. For example, In Figure 2 there are two Sexpressions from generation 1 where nodes 4 and 6 have been randomly selected to be subtrees. Crossover cuts off these subtrees from each of the Sexpression's and swaps them. This creates two entirely new Sexpression's that are similiar to thier parents. This is very similiar to regular reproduction where a child is made up of a combination of its parents genes. This ensures variety and adaptability. Hopefully, if you have setup everything correctly, then as the generations crank along then the entire population should keep getting more fit until you finally reach a solution. This solution may not neccessarily be THE correct answer. It might simply meet some predefined criterion. Most of the optimization problems are done this way.
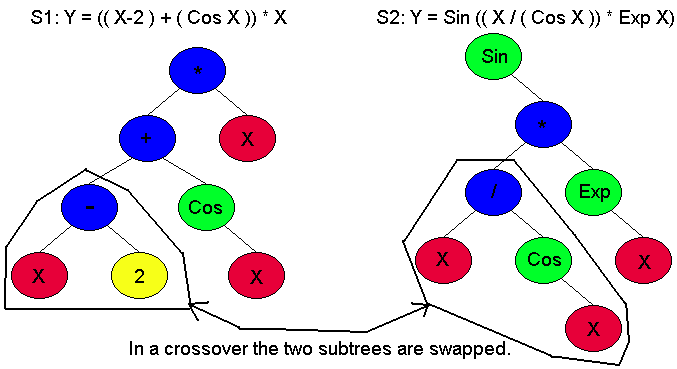
Figure 2: Initail Sexpression's
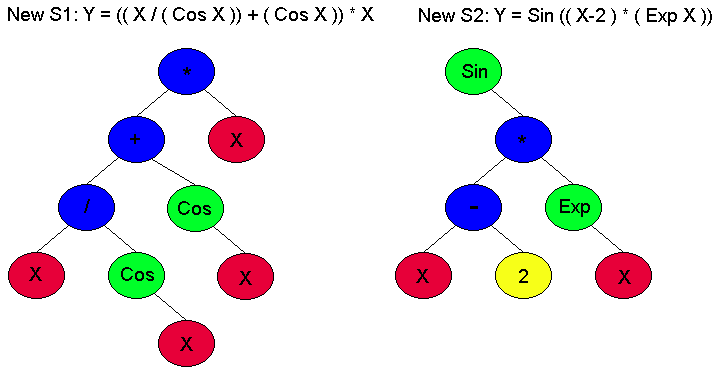
Figure 3: Sexpression's after crossover
The Genetic Algorithm (GA) is quite similiar to the GP's described above. However, instead of using the tree structure of an Sexpression, they use a string of binary numbers that more closely resembles a DNA coding. The various answers or solutions to the problem are encoded in the binary values of the string and the GA program interprets those values and assigns each string a fitness value. Reproduction then occurs like before, except instead of choosing two random nodes to swap subtrees in crossover, only one position of the string is chosen. The two strings are broken in half at that position and the substrings are swapped. Also, another operator called mutation is used in GA's. Basically, each generation some randomly chosen bits in some strings are inverted. This is something similiar to the errors that occur in the replication of human DNA.
One of the main advantages is that with the GP method it is much easier to understand and setup the actual problem to be solved. You simply decide what type of nodes that you will need, and decide how you will judge fitness. In GA's you must set up the strings and encode the variables, and decode the variables. This is time consuming and very difficult to read. With GP's you can practically read the answer right off the screen.
However, The biggest advantage comes in the area of pre-mature convergence. One of the problems with these types of programs is that they can tend to converge to a sub-optimal solution. For instance, if you think of the entire space of solutions as landscape where the altitude is determined by how close you are to the correct solution, then you will have a landscape with peaks and valleys where the peaks are places that are closer to the correct answer. Now as the program goes through the generations it should start climbing up the peaks to get to the highest, and thus most correct, value. Unfortuanetly, sometimes as it is climbing it reaches the top of a peak and gets stuck. This is because in order to reach the top of a higher peak, it will have to actually go down from this peak, and thus become LESS fit. It does not want to do that. Convergence to a subpeak is usually caused because there is not enough variety in the population, so one or two individuals dominate the next generations and kill off everyone else. The only way that GA's can overcome this tendency is to use the Mutation operation to try and add new variety to the population. However, there is no need to use mutation at all in GP because there are actually two forces at work. The first moves the system towards convergence, and the second pushes it towards greater variety. Lets look at an example. If you are using a GA and one individual comes to dominate the population then it is much more likely that that member will crossover with another copy of itself. Since only one position is chosen in the string to perform crossover, then when you swap the substrings you will end up with EXACTLY the same two strings. However, in GP if an individual mates with itself then it is unlikely that the two nodes chosen within that Sexpression will be the same. And if the nodes are different then you will end up with two entirely new Sexpressions. This means that in GP if one individual does begin to dominate future generations, then the operation of crossover garuntees that variety will remain, and thus fight off the tendency to pre-mature convergence.
The main disadvantage of GP has been that if it is not done in Lisp, it is very difficult to program. And I don't know about you, but the taste of Lisp I got was very sour indeed. It is a tedious and boring language. More important though is the fact that, relatively speacking, very few people actually use that language and is not very widespread. Setting up a GP program in another language is a gargantuan task. I would never have dreamed of trying to put this library together without the incredible tools of C++ like templates and polymorphism because it would be almost impossible. Hopefully, this library will solve this problem though, and make Genetic Programming fast, easy, and fun.
This program relies HEAVILY on polymorphism. If you have trouble with that concept then you will have a lot of trouble understanding this library. The basic unit is obviously the Sexpression (Sexp). This is a tree template where each of the nodes are sockets where you can put any of the different kinds of nodes. The user has to write his nodes, a class to evaluate fitness and classes to simulate the Sexpressions. All of these are derived from base classes that are provided and the program uses this to perfrom all of the different operations. My test program is the curve fitting application discussed above. However, the program I am really looking forward to is one that simulates an ant colony. It is meant to show the principles of emergent behavior. The idea of the program is to try and get a colony of ants to cooperate in order to forage food. When a real ant finds food it picks some of it up and carries it back to the nest, and drops a pheremone trail so that other ants can find the food. As more ants go over the trail it makes the trail persist longer. When the food is all gone then the pheremone trail starts to disappear. The Sexpression is used as the brain of an ant. It has various nodes like "If food ahead", "Move forward", "Pick up food", "Drop Pheremones", and so on. At each time step all of the ants use the Sexpression to determine what it will do next. Fitness is determined by how much food a given colony can bring back to the nest. Gradually over time the ants in the colony start working together in way that is identical to natural ants. This is called spontaneous emergent behavior because the rules that the individual ants use are not explicitly programmed into them. They are evolved over time, and thus emerge. It has been found that very complicated behavior patterns such as this and flocking and other things can be described by a set of very simple rules.
If you are interested in learning more about genetic programming, then be sure to read the book Genetic Programming By John R. Koza.

This page hosted by
 Get your own Free Home Page
Get your own Free Home Page







 Send me mail at:david_cofer@oocities.com
Send me mail at:david_cofer@oocities.com