OSCILLATIONS Energy interchanges during simple harmonic motion. EXAMPLES OF SHM
|
The SHM of a simple pendulum, with its constant period has
been utilised to power clocks. There are two forces acting on the bob (ingnoring air resistance), the weight of the particle m g and
the reaction of the string nad the force that causes it to accleration towards its equilibrium. This restoring force is the one that is responsible for
the SHM, it is equal to the component of m g perpendicluar to the string, i.e. if the string is at an angle O it is m g sin( O ).
this by Newton's 2nd law is equal to m a, hence acceleration equals g sin( O ), but this is not an
SHM equation. If we cosider a situation when O, the angle of inclination is very small compared with
the length of the string l, then we can assume the segment of the circle to be a triangle and write sin( O ) = x / l
and then |
|
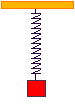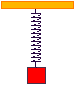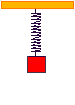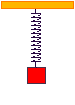
A mass suspended on a spring, undergoes SHM. By Hooke's law the tension in the spring is equal to k l, where
l is the extension. The force accelerating the particle will be equal to this minus the weight, m g ,of the particle. At its equilibrium postion k l = m g ,
at any other point x away from the equilibrium postition the accelerating force will be k ( l + x ) - m g and as we have already found k l = m g ,
by newton's 2nd law |
ENERGY CHANGES
We can also consider S.H.M. in terms of energy, for example in the above to examples there is an interchange between gravitational potential
energy and kinetic energy. For undamped SHM there is no loss of energy and the sum of kinetic and potential energy is a constant. Consider a
general situation: Kinetic energy is equal to 1/2 m w2( r2 - x2)
Potential energy is equal to Workdone in moving to x, which is the
integral of force with respect to distance, 
m w2 x dx
which is equal to 1/2 m w2 x2.
So the total energy at any displacement is 1/2 m w2( r2 - x2) -1/2 m w2 x2
= 1/2 m w2 r2
and is hence independant of the displacement x, so a constant throughout the motion.
