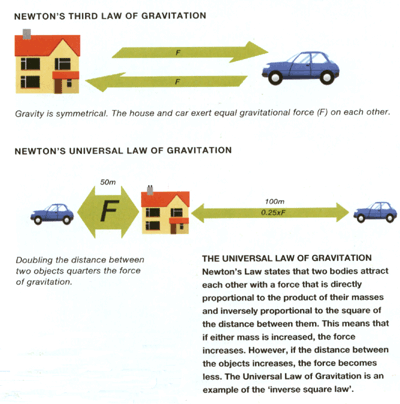
Newton's Law of Gravitation states the following equation:

Where:
F is the attractive force
G is the gravitational constant (6.67x10^-11 Nm²/kg²)
m₁ and m₂ are the masses of the two objects
d is the distance between to the two masses from the center of gravity

As a rule, this equation is usually applied to relatively large spherical shaped masses with distances of two or three times their diameter away from each other. This law affects all objects in the universe and is therefore known as the universal law of gravitation.

In this case, the attraction of irregular shaped objects like asteroids is more complex. Every part of matter on an irregular object will attract every part of matter in another object. The difference between a spherical and irregular object is that in a spherical object, the pull of gravity (ex: Earth) is about uniform in strength throughout. In the case with an irregular object, it could be said that a point called the center of gravity in the object could be considered as where all the force of gravity is acting upon.

Newton's second law of motion gives the following equation:

Where:
g_h is the gravitational force at a specific height above the ground.
g is the gravitational force on the Earth's surface
R is the Earth's radius (spherical shaped)
h is the altitude or height above the surface
(R+h) is the distance from the Earth's center

With the use of Newton's gravity equation, it is possible to calculate the attractive force and to see that gravity will vary depending on the different altitudes or distances between the centers of the two masses. (An example of this case could be the distances between an asteroid and the Earth)

Because the Moon has significantly less mass than Earth, the weight of an object on the Moon's surface is only one-sixth the object's weight on Earth's surface. This graph shows how much an object that weighs w on Earth would weigh at different points between the Earth and Moon. Since the Earth and Moon pull in opposite directions, there is a point, about 346,000 km (215,000miles) from Earth, where the opposite gravitational forces would cancel, and the object's weight would be zero.

In general, all objects in the universe have a gravitational attraction with other objects. In the asteroid belt between Mars and Jupiter, it is clearly shown that no matter how small or large an object (Ex: Asteroids & Planets) is, they will exhibit a gravitational and attractive force towards other objects.