2.4.2 Triangulation
 

Sie scheint das älteste wissenschaftliche Messverfahren zu sein, wird sie doch angewendet, seit die Beziehungen in einem rechtwinkligen Dreieck bekannt sind.

Prinzip

nach [1 i)] [3] [11]

Abbildung 2.3: Triangulation Quelle [3]

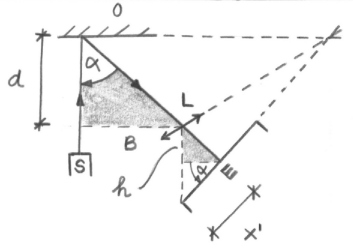
Die Distanzmessung beruht auf dem Vergleich von ähnlichen Dreiecken. Das eine Dreieck ist das Objekt-Dreieck, aufgespannt zwischen Objekt und Linse, das andere ist das Bild-Dreieck, aufgespannt zwischen Linse und Empfänger. Eine Linse wird zur Abbildung des auf dem Objekt diffus^xvi reflektierenden Signals benötigt, damit sich Ein- und Ausfallwinkel unterscheiden. Nur so kann eine Tiefenauflösung erzielt werden. Zusätzlich wird der Empfänger um einen bestimmten Winkel gedreht. Damit soll die Scheimpflug-Bedingung berücksichtigt werden. Diese besagt, dass die beste Focussierung erzielt werden kann, wenn sich die Objekt-, Linsen- und Empfängerebene in einem Punkt schneiden. Daraus ergibt sich folgende Formel [3] :

 (2-4)

Offensichtlich ist, dass die Distanz umgekehrt proportional zur Messgrösse ist.

Eindeutigkeit

Der Triangulation sind vordergründig keine Grenzen gesetzt. Die Anpassungsfähigkeit des Verfahrens an die zu messende Distanz (Skalierbarkeit) ist ein grosser Vorteil. Der Messbereich wird lediglich durch die Grösse des Empfängers begrenzt.

Ein Nachteil kann jedoch sein, dass das Verfahren auf relative Messungen beschränkt ist. Damit eine Distanz ermittelt werden kann, muss zuerst mit einer Referenzmessung der Nullpunkt bestimmt werden.
 
Auflösung / Genauigkeit