back | home | abstract | contents | next chapter

          A
          Parameter Calculation
For the proper experimental values exist a relation between the codebooksize, the dimension, the average number of codevectors submit to the whole distortion computation I and the average number of iterations l . As discussed in chapter 3.2.2 can we assume an I proportional to the codebooksize N and constant l = 1. The following calculations give the numerical values.
codebooksize N
64 128 256 512
dimension k 4
131.2
254.4
497.6
8
212.8
415.2
808
1608
16
379.2
739.2
1409.6
2705.6
32
812.8
1494.4
2739.2
5315.2
64
1670.4
3027.2
5619.2
10489.6
 
Figure 9: The average number of comparison per vector versus the dimension for different codebooksizes.
 
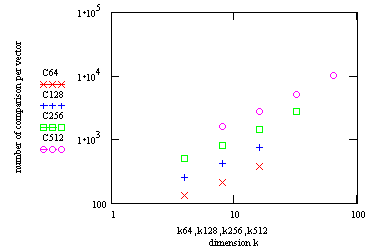
The linear relationship between the average number of comparison per vector and the dimension is approximated by a linear regression described by the following equation.

                 (A-1)

The slope corresponds to the average number of codevectors submit to the whole distortion computation and the shift corresponds to the average number of iterations multiplied by the diminished codebooksize. With increasing codebooksize the slope increases too, hence I must be a function of N. The following table resumes the values.
N I I/N l
64
20.685
0.323
1.108
128
40.414
0.315
1.054
256
80.100
0.312
0.921
512
159.794
0.312
0.669
As we can see is there a linear relationship between I and N and further that l is approximately constant. There l is constant for the codebooksizes N = 64, 128 and 256 but decreasing for N = 512. In the view that our model is restricted by two parameters, we assume the average number of iterations l as constant. So we propose the following parameters to modeling the partial search algorithm.

This parameter are valid for codebooksize from N = 64 up to 512 and dimensions from k = 4 up to 64 and its combination shaded in the above table.

begin chapter | next chapter