back | home | abstract | contents | next chapter
          3
          Modeling Unconstrained Vector Quantization Complexity

     
     
     
          In the precedent chapter has been presented four different methods for vector quantization: the exhaustive search and the partial distance search algorithm as full search methods and the triangular inequality and vector-to-scalar mapping elimination as fast search methods. Further we have estimated for each algorithm a theoretical computational complexity, the number of operations, necessary to encode a vector. For the exhaustive search this complexity is independent of the codevectors. Where for the partial distance search method this distribution directly influence its efficiency. The fast search methods on the other hand exploit this distribution to make an estimation for the codevector and then to search in its neighborhood. In the presented formulas we have assumed for this search the exhaustive search algorithm, but its obviously, that for practical applications the partial distance search algorithm or an other appropriate algorithm can be used to further reduce the complexity. Therefor we try to model in the following chapter the partial search algorithm. This model when can be adjoined to the theoretically attainable inferior limit for each method to get an approximation for the computational complexity.
           
          Two approaches are presented in the following. The first is to use the experimental results presented by the different authors to get a model; the second is to implement the partial search algorithm and to estimate the model ourselves.

          begin chapter | next chapter


      3.1 Complexity Structure of the Partial Search Algorithm
       

          The partial distance search algorithm is a full search method. This means, that each of the codevectors in the codebook is affected by the search. Therefor the encoding of a source vector needs a minimum number of operations depending of the codebooksize N and its dimension k. This contribution to the complexity is independent of the distribution of the codevectors. Each distortion calculation is performed by cumulating the squared difference between the pixel of the source vector and the codevector. There this accumulation has maximal k iterations, which is the dimension. The exit condition for this loop is when the accumulated distortion is greater than the minimal known distortion. When this is performed depends of the pixel values and hence of the codebook distribution. So only an average number of iteration can be considered.
           
      independent part dependent part
      number of additions S per vector 2k+2(N-1) 2(N-1)(kC-1)
      number of multiplication P per vector k+N-1 (N-1)(kC-1)
      number of comparisons C per vector k+N-1 (N-1)(kC-1)
      total 4k+4(N-1) 4(N-1)(kC-1)
           
          There the average number of iterations is restricted to 1£ kC £ k. When searching for a complexity model the independent part can always be subtracted. As we have seen, is this substantial for large codebooks and small dimensions. So to get a model for partial distance search algorithm it is necessary to know the average number of iterations for different codebooksizes and dimensions

          begin chapter | next chapter


      3.2 Parameter Estimating

      3.2.1 Existing Experimental Results

         
          The following table resumes the average number of addition, multiplication and comparison per pixel for different authors. The selection is restricted to a codebooksize of N = 256 and 512 and a dimension of k = 8 and 16.
         
         
        source N k operations per pixel inferior limit min max
        [25] 512 16 addition 65.875 58.4 144.7
        multiplication 32.9375 45.2 88.3
        comparison 32.9375 45.2 88.3
        [13] 256 16 addition 33.875 71.21 97.56
        multiplication 16.9375 43.61 56.78
        comparison 16.9375 43.61 56.78
        [18] 256 16 addition 33.875 222.6
        multiplication 16.9375 111.3
        comparison 16.9375 111.3
        [12] 256 16 multiplication 16.9375 57.865
        [26] 256 8 addition 65.75 106.78 154.98
        multiplication 32.875 69.39 93.49
        comparison 32.875 69.39 93.49
        [8] 256 8 multiplication 32.875 50.5 145.2
        [7] 256 8 multiplication 32.875 66.00 68.3
         
         
          First to note is that all authors quote Bei and Gray [7] as the source for their algorithm. If we take a closer look to the above-established relations for this algorithm, we notice that the number of comparison and the number of multiplication should be the same and that the number of addition is the double of these. But the experimental results, except for Poggi [18], violates all the relation between the number of addition and the number of multiplication and the number of comparison. Further Poggi [18], Lo and Cham [13] and Ngwa-Ndifor and Ellis [12] are using the same test image, but Poggi obtains a result, which is about two times greater. This is only possible if the codebook is ordered for the worst case, like the results by Paliwal and Ramasubramanian [8] show. Their minimum value is for an ordered codebook and the maximum value is for an inverse ordered codebook. Finally Lai and Tai [25] obtain a minimum value, which is inferior to the theoretical limit. So there is a fort inconsistency between the maden considerations and the experimental results. We don't know their particular implementations, a difference could only result if instead of the Euclidean squared norm an other norm is used for the distortion computation. Anyway we try to estimate with these data an average number of iteration. This for having a coarse idea about its possible dimension.

          begin chapter | next chapter

          Average Number of Iterations
           

          With the help of the expressions for the number of operations for addition, multiplication and comparison we can compute the average number of iteration for each combination codebooksize N and dimension k. There the expected values should be restricted to 1£ kC£ k.
           

         
        source N k average number of iterations based on min max
        [25] 512 16 addition 0.883 2.234
        multiplication 1.384 2.734
        comparison 1.384 2.734
        [13] 256 16 addition 2.171 2.998
        multiplication 2.674 3.500
        comparison 2.674 3.500
        [18] 256 16 addition 6.921
        multiplication 6.921
        comparison 6.921
        [12] 256 16 multiplication 3.568
        [26] 256 8 addition 1.644 2.400
        multiplication 2.146 2.902
        comparison 2.146 2.902
        [8] 256 8 multiplication 1.553 4.524
        [7] 256 8 multiplication 2.039 2.111
         
         
          We find a range for the average number of iterations between 0.883 and 6.921. The inconsistency still remains for the above-discussed reasons. For the following estimation the values of Poggi [18] are omitted. They are the only ones, who match with our assumptions, but they are too large by factor two compared to the over values. Also the values of Paliwal and Ramasubramanian [8] are not considered, because they are obtained by ordering the codebook, which isn't the case for the other values. So the range is reduced from 0.883 to 3.568.
           
          At a first glance no value is matching for all combinations. There is no reason to be so, because the average number of iterations is influenced by the distribution of codevectors in the codebook. Instead to search for an appropriate distribution, we introduce one more parameter. So we assume an unknown distribution characterized by two properties. Following the modified expressions for the number of addition, multiplication and comparison.
         
         
        number of additions S per vector 2(kI+(N-I)l )
        number of multiplication P per vector kI+(N-I) l
        number of comparisons C per vector kI+(N-I) l
        total 4(kI+(N-I) l )
         
         
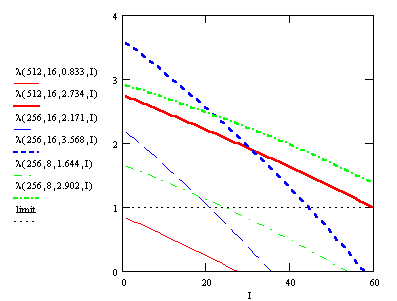
          The parameter I is the average number of codevectors needing the complete distortion computation, so satisfy the condition d2 £ dmin2. Where l is the new average number of iterations, which should be inferior to kC. For l = kC and I = 1 we obtain the same expressions as used up to now. Therefor this two parameters are not independent and it can be derived a relation between kC, l and I for a given codebooksize and dimension. The following Figure 3 represents the relation between the parameters for different N and k and the corresponding maxima, thick line, and minima, thin line, values for the average number of iterations listed in the above table.
           
          For the same codebooksize to dimension proportion nearly the same slope for the maxima-minima ribbon exists. Further that this slope increases with the diminution of the proportion. An evident relationship between I, l and N, k can't be recognized, but the values have to lie in the plane such that they are limited by the lines for kC = 1.644, 2.171, 2.734 3.568 and the limit.


          Figure 3: Average number of iterations l versus average number of codevectors I needing the complete distortion computation for different codebooks and its experimental average number of iterations kC.
          begin chapter | next chapter
           
      3.2.2 Proper Experimental Results
         
          To obtain reasonable results we have implemented the algorithm ourselves. The number of operations has been measured for different codebooksizes N and dimensions k. In the following we describe the used algorithms and give an interpretation of the established values.

          begin chapter | next chapter

          Used Algorithm

          For every combination codebooksize and dimension a codebook has to be computed. We used for that the LBG-algorithm presented in [6]. With the already described exhaustive search algorithm, a training set of vectors and set of initial vectors a codebook is generated, such that the initial codevectors converge to the codevectors representing a minimal overall distortion for the training set. This is an iterative process, at each repetition each training vector is associated to its nearest neighbor codevector resulting in N subsets called Voronoi regions. When for each subset the centroid is computed. These vectors constitute the new codevectors and the procedure can be repeated once more. To save computation time we made ten iterations and didn't execute the calculations until the minimum distortion has been reached. The measured distortions state, that this number of iterations is sufficient and that the distortion is near enough to the minimum. For the initial codevector we selected vectors of the training set with a distribution along its squared Euclidean norm. The vector quantization is obtained by using the partial distance search algorithm as described in 2.1.2. The number of operations for addition, multiplication and comparison was measured by incrementing each a counter. For further details the corresponding MATLAB files are listed up in the annex B.

          As the training set we used the images peppers, baboon, barb, gold and as the source image lena.

          begin chapter | next chapter

          Experimental Results

          The following table resumes the measured average number of multiplication or comparison operations per pixel. As discussed above, the number of addition operations are these values multiplied by a factor two and the total number of operations are these values multiplied by four.
           
           

              codebooksize N
              64 128 256 512
          dimension k 4 32.8 63.6 124.4 -
          8 26.7 51.9 101.0 201.0
          16 23.8 46.3 88.1 169.1
          32 25.4 46.7 85.6 166.1
          64 26.1 47.3 87.8 163.9
           
           
          The experimental results are in the same range as the results by Poggi [18]. This proofs that the other authors are using a different partial distance search algorithm than described by Bei and Gray [7].

          Before giving an interpretation, there is to note that only large codebooks with small dimensions are for practical use. So only vector quantization resulting in a small distortion is applied. The following Figure 4 shows the growing degradation. The first picture is the original. The others are obtained by quantizing with a codebook of size N=512 and the dimension k = 8 for the upper right, k = 16 for the bottom left and k = 32 for the bottom right. So with increasing dimension the bit rate is decreasing. This is equal to a loss in information as it can be observed in the following pictures.

          The growing degradation states also in the experimental results. With increasing dimension the complexity passes by a minimum. So for the following parameter estimation, only the shaded values in the table are considered.



          Figure 4: Vector quantization with the partial distance search algorithm for different codebooks. Upper left: original picture. Upper right: codebooksize N = 512, dimension k = 8 Bottom left: codebooksize N = 512, dimension k = 16 Bottom right: codebooksize N = 512, dimension k = 32

          begin chapter | next chapter

          Average Number of Iterations
           

          As for the existing experimental results we compute the average number of iterations kC. Because of the proportionality between the number of addition operations and the number multiplication and comparison operations only one value is obtained. The values are listed up in the following table for the considered codebooksizes and dimensions.
           

       
      codebooksize N
      64 128 256 512
      dimension k 4 2.019 1.972 1.936 -
      8 3.264 3.206 3.137 3.131
      16 5.790 5.707 5.465 5.263
      32 - - 10.616 10.339
      64 - - - 20.402
       
       
          We state, that for a given dimension k the average number of iterations is nearly constant. For increasing codebooksize the values are slightly decreasing. Further that with doubling the dimension k the average numbers of iterations have the tendency to double the values too. If we assume kC constant for a given dimension k, it still rests to find a relation between the kC for a given codebooksize. Again we use the parameters I and l to find an appropriate description. The following Figure 5 shows these parameters for the above computed average number of iterations.




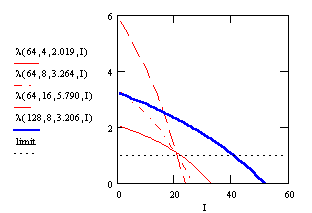
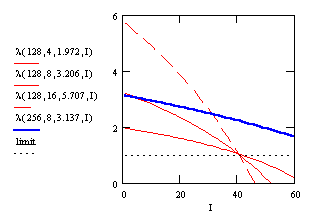
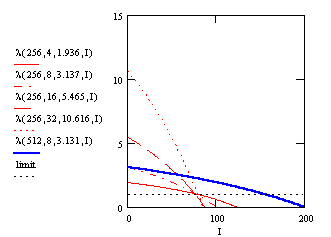
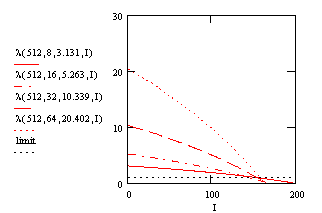
          Figure 5: Average number of iterations l versus average number of codevectors I needing the complete distortion computation for different codebooks and its experimental average number of iterations kC
           
           
          For a given codebooksize the graphs for different dimension cross approximately in one point near the limit. Further we have a similar slope for the same codebooksize to dimension proportion. Due to the doubling of kC for a given codebooksize, the parameter I at the crossing point is also doubling with increasing N. The proportional factor between I and N is about 0.316. So we propose the following parameters to modeling the partial search algorithm.



       

          The calculation made in annex A shows, that the proposed value for I is constant for the different codebooks. With a constant I the parameter l can be derived. These values are only approximately constant; they decrease with increasing codebooksize. Anyway we assume l constant in view, that we suppose a model for the partial distortion search algorithm with only two parameters. Following the final expressions for the number of addition, multiplication and comparison.
       
       
      Number of additions S per vector 2N(0.316k+0.684)
      Number of multiplication P per vector N(0.316k+0.684)
      Number of comparisons C per vector N(0.316k+0.684)
      total 4N(0.316k+0.684)
       
       
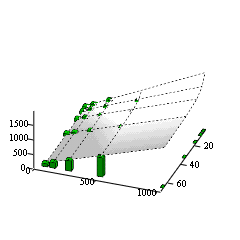
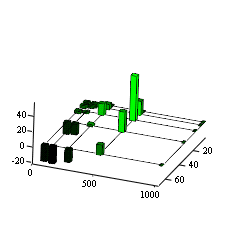
          This relations are valid for codebooksize from N = 64 up to 512 and dimensions from k = 4 up to 64 with the best matches for the combination shaded in the above table. The following Figure 6 shows the total number of operations. The plane is our proposed model, where the bars are the proper experimental results. The next Figure 7 shows the error. The difference is maximal for the codebooksize N = 512. The reason is, that we fixed the average number of iterations, but in fact it is decreasing with increasing codebooksize.
           
          Figure 6: Total number of operations for the partial distance search algorithm. The plane represents the proposed model for the computational complexity. The bars represent the measured results. The x-axis is the codebooksize in a range from 64 to 1024. The y-axis the dimension in a range from 4 to 64.
      Figure 7: Difference of the total number of operations between the model and the measured results
       
       
          Finally we found with the above relations a superposition function, which can be adjoined with the inferior limit functions for the triangular inequality elimination and the vector to scalar elimination method. The model is only valid if the size of the expected subsets of codevectors is in the range from 64 to 512. For practical application the model has to be extended to smaller codebooksizes.
          We have now also the weighting function to obtain the partial distance search complexity from the exhaustive search complexity. This function represents also the gain in complexity by passing from one method to the other. The following Figure 8 shows this relationship.

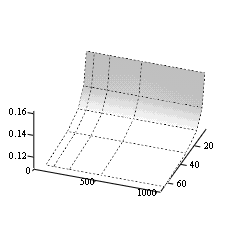
          Figure 8: The gain of complexity reduction by passing from the exhaustive search algorithm to the partial search algorithm
           
           
          The gain of complexity reduction is by a factor in a range from five to ten. To note is that the gain is approximately constant for a given dimension. With increasing dimension the gain is also increasing but the bit rate is decreasing as we have seen above. So the quality degradation sets a limit in choosing the codebooksize.

          begin chapter | next chapter
           

      3.3 Conclusion
A model for unconstrained vector quantization complexity, in especially for the partial distance search algorithm, is proposed with two parameters. One parameter is the average number of codevectors submitted to the complete distortion computation, the other parameter is the average number of iterations necessary to compute the exit condition. So only the partial distortion is affected in the search process. The restriction to two parameters limits the model in its range of application. Therefor only codebooks with the size N = 64 up to 512 and dimension k = 4 up to 64 can be considered. To get a more general model, who can also be combined with the other search methods, the experimental results must be extended.

begin chapter | next chapter