- back
| home | abstract |
contents
| next chapter
Unconstrained Vector Quantization
- In the following chapter we take a closer look to unconstrained vector
quantization. So the codebook used for the encoding and decoding is optimal
in the sense that the overall distortion is minimal. There the distortion
between an input vector x and a codevector yi
is measured by the mean squared error.
- But the minimum can only be reached, if for a given input vector the
nearest neighbor codevector can be found. There exist different search
strategies that will be discussed now by its algorithm and computational
complexity. There the computational complexity is the number of executed
operations, such as addition, multiplication and comparison, until the
nearest neighbor is found.
2.1 Full Search Vector Quantization
- The simplest way to find the nearest neighbor codevector is to compute
for a given source vector the distortion for each of the N possible codevectors
and to choose the codevector with the minimal distortion. The exhaustive
search algorithm and the partial distance search algorithm exploit this
idea.
2.1.1 Exhaustive Search
Algorithm
- The algorithm, derived from the algorithm of Linde, Buzo and Gray [6],
is based on an unordered codebook, a set of N codevectors with dimension
k. To each codevector is associated an index i. A given input vector is
encoded by searching the codevector with minimal distortion. So at the
begin of the searching there are assumed a minimal distortion dmin2,
who is greater than every possible distortion, and an index imin,
who is out of the possible index range. For the first codevector the distortion
is calculated by the accumulation of the squared differences between the
k components of the vectors. This distortion is assigned to dmin.
Then ongoing for each codevector the distortion is computed and if the
current distortion is smaller than the minimal distortion yet found in
the search, the current index is assigned as the minimal index. After the
N calculations the index for minimal distortion is found. The decoding
is then to look up in the codebook for a given index i the associated codevector.
Algorithm
given
- codevectors yi
there i=1...N
source vector x
dmin2
= ¥
imin = NIL
for i = 1 to N
- d2 = 0
for j = 1 to k
- a = xj - yij
b = a × a
d2 = d2 + b
if d2 < dmin2
- dmin2
= d2
imin = i
The complexity can be easily derived from the algorithm. In the following
table, the first column are the values for the above algorithm, the second
column are the theoretical values for the mean squared error. So for a
codebook with N codevectors of dimension k:
| number of additions S per vector | 3Nk+N | (2k-1)N |
| number of multiplication P per vector | Nk | Nk |
| number of comparisons C per vector | Nk+2N | N-1 |
| total | (5k+3)N | 3Nk-1 |
- The subtraction is thereby considered as an addition. Further for each
iteration an addition and a comparison operation is assumed.
2.1.2 Partial Distance
Search Algorithm
- To find the nearest neighbor it is not necessary to calculate the complete
distortion as in the exhaustive search algorithm. Observe that if the minimum
distortion yet found in the search is bigger than the accumulated distortion
when the distortion calculation can be stopped and it can be continued
with the next codevector in the codebook. Such an algorithm as been proposed
by Bei and Gray [7]. So the partial distance
search also named partial distance elimination, algorithm is the exhaustive
full search algorithm with the comparison during the distortion accumulation.
This local increase of complexity, the repetition of the comparison operation,
is compensated by the suppression of a larger number of additions and multiplication
this resulting in a smaller overall complexity.
Algorithm
given
- codevectors yi
there i=1...N
source vector x
dmin2
= ¥
imin = NIL
for i = 1 to N
- d2 = 0
for j = 1 to k
- a = xj - yij
b = a × a
d2 = d2 + b
if d2 > dmin2
- next i
dmin2 = d2
imin = i
Complexity
For this algorithm the complexity can not be calculated à priori, because of the uncertainty in the exit condition. This depends of the distribution of the codevectors in the codebook, which is normally not known. So a mean value kC is introduced for the number of iterations in the distortion accumulation loop to correct the number of additions and multiplication. The following table resumes this, there are N the number of codevectors, kC the average number of iterations once the first codevector in the codebook is tested and k the vector dimension. The first column is the expression for the partial search algorithm without considering the iteration operation. Therefor we can it compare to the exhaustive search algorithm represented in the second column.
| number of additions S per vector | 2(k+(N-1)kC) | (2k-1)N |
| number of multiplication P per vector | k+(N-1)kC | Nk |
| number of comparisons C per vector | k+(N-1)kC | N-1 |
| total | 4(k+(N-1)kC) | 3Nk-1 |
- The average number of iterations is restricted to 1 £
kC £ k. In the next chapter
will we discuss how to approximate the average number of iterations kC
by modeling the codevector distribution.
An improvement in search time can be achieved by ordering the codevectors in the codebook by its size of Voronoi regions, such that the probability to find a codevector at the begin of the codebook is increased. This has been showed by Paliwal and Ramasubramanian [8]. The improvement is an up 10% lower complexity for codebook with N = 256 and k = 8 compared to a search with an unordered codebook.
2.2 Fast Search Vector Quantization
- In the case of the partial search algorithm the ordering of the codebook
by its size of Voronoi regions reduced the complexity. This is one idea
behind the fast search vector quantization and leads to the vector-to-scalar
mapping elimination methods. Instead of using the Voronoi region size,
a property of the source vectors are used to order the codebook. So the
codevectors are ordered by its associated criterion. To encode a given
source its proper criterion is computed, when look up in the codebook for
the codevector, whose criterion is matching most. Once found this codevector,
the index is searched in its neighborhood. The other idea is to consider
only a subset of codevectors. The selection which codevector belongs to
the subset is based on a maximum distortion criterion. So to encode a source
vector is to calculate its maximum distortion criterion, then selecting
the matching codevectors and to search in this subset the index. We will
see that this maximum distortion criterion is based on the triangular inequality.
In the favorable case only a fraction of the codevectors in the codebook are affected by the search algorithm and therefor complexity is reduced. In worst case both methods are searching in the whole codebook. As this is rare the case, often the searching range is fixed to a maximum value. In this case the vector quantization is no more optimal and a slight decrease in performance is to take into account. Chang et al. [9] and Wilton and Carpenter [10] have both stated for the vector-to-scalar mapping elimination method a degradation of performance of about 0.5 dB in SNR compared to the exhaustive search algorithm.
For fast vector quantization the complexity can not be calculated à priori, because the search range depends of the distribution of the codevectors in the codebook. Anyway in this case we can notice that the complexity is composed by a fix part, the computation of the criterion, this is also named calculation overhead and a variable part, the search for the nearest neighbor.
2.2.1 Triangular Inequality
Elimination
- The distortion can be computed as a distance between two vectors in
a k-dimensional space. Then the condition for the nearest neighbor codevector
y
by a given source vector x is
- So every distance between the source vector and a codevector is larger
or equal than the distance between the source vector and its optimal codevector.
In the case of the exhaustive full search algorithm it requires N vector
distance computations to fulfil this condition. By using the triangular
inequality and a set of reference vectors, fixed points in the space, the
number of distance computations will be reduced. Applying the triangular
inequality between the source vector x, the optimal codevector y
and a reference vector r yields
- We obtain together with the nearest neighbor condition (2-1)
and by replacing the codevectors yi by the reference
vectors
rn
- There R={r1,...,rn,...,rJ}
is a set of vectors with the size equal or less than the codebook. But
the optimal codevector is not known. Instead we choose a codevector ym
in its neighborhood. Further the codevectors yn themselves
are used as the reference vectors. So finally we obtain the following two
elimination conditions, who are both equally
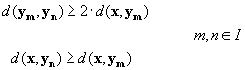 (2-4)
(2-4)
- The second condition can be regarded as a hypersphere with the radius
d(x,ym), the maximum distance criterion, and the
center x there only the codevectors inside the sphere are considered
for the search for y.
- How to choose the codevector ym is based on an inherent
property of the image vectors. It has been stated but not proofed by Huang
et al. [11] that the Euclidean vector
norm d(x) is a sufficient criteria cx. So the norm of
codevector ym matches best with the norm of the source
vector x . To simplify the search for ym, the
vectors in the codebook are sorted according to its criterion in descent
order. An other method is to use the correlation between neighbor image
vectors. With the known optimal vectors y the codevector ym
is estimated. Such a prediction was elaborated by Ngwa-Ndifor and Ellis
[12] and applied to the triangular inequality
method by Lo and Cham [13].
- So to encode a source vector x its criteria cx is
computed, then looked up in the codebook for the codevector ymwith
the nearest criteria cm. The distance d(x,ym)
is calculated and with the help of the first condition (2-4)
a subset of codevectors is generated by considering only the codevectors
yn who pass the test. There the distances between the codevectors
d(ym,yn) are precalculated and stored in a matrix.
Once the subset is identified the search for the optimal vector y
is performed, as described in full search vector quantization. If the optimal
codevector isnít in the set, when the maximum distance criterion has to
be enlarged and the elimination and search procedure have to be repeated.
- The method above was proposed by Huang and Chen [14],
who is a simplified version of a method proposed by Vidal [15]
using a hyperannulus instead of a hypersphere. A combination of both methods
was proposed by Huang et al. [11], where
Li and Salari [16] generalized these methods.
- To note is that all this algorithms are using a fixed range. The mentioned
authors hadn't compared the overall distortion between their methods and
the exhaustive search algorithm. So we don't know the suboptimality, if
there is any, of triangular inequality elimination method.
Algorithm
The variety of triangular elimination methods permits only a general description, which can be subdivided in the steps approximation, elimination and search. Following is this illustrated for the above-described method.
given
- codevectors yi
there i=1...N
reference vectors yn there n=1...N
source vector x
precalculation
- - determine criteria ci
for each codevector yi
- sort codevectors yi by ascending order of ci
- determine distance matrix of dimension NxN
by calculating d(yi,yn)
approximation
- - determine criteria cx
for the source vector x
- identify codevector ym with cm most nearly to cx
elimination
- - determine distance d(x,ym)
- identify subset which contains all codevectors yn
satisfying the condition d(ym,yn)³ d(x,ym)
search
- - search nearest neighbor codevector
y
in the subset
by a full search algorithm
if y is in the subset
- - assign imin
- - enlarge ym
and continue with elimination
In view of the general description the complexity can only be estimated. We have seen that the triangular inequality elimination method contributes to the complexity a fix and a variable part. There the fix part includes the approximation and the elimination and the variable part includes the search.
- If we consider the Euclidean vector norm for the criterion computation,
when we need k-1 additions, k multiplication and 1 square root. The square
root can be omitted by using the squared Euclidean vector norm, so this
operational isn't considered. The identification of the approximation vector
needs log2(N) comparisons when using a binary search algorithm.
For the distance we need (2k-1) additions and k multiplication. Further
we need N comparisons for the subset identification and 4NSk-NS-k
total operations for the nearest neighbor search using the exhaustive search
algorithm. There NS is the size of the subset, who is much smaller
than the codebook size N. Huang et al. [14]
stated in their experimental results an NS = 45.5, 75,7 and
177.3 for the codebooksize N = 256, 512 and 1024 with dimension k = 8.
The following table resumes the above estimations.
| fixed part | variable part | |
| Number of additions S per vector | 3k-2 | (2k-1)NS |
| Number of multiplication P per vector | 2k | NSk |
| number of comparisons C per vector | N+log2(N) | NS-1 |
| total | N+5k-2+log2(N) | 3NSk-1 |
- As we can see, we have obtained an impressively computational complexity
reduction. The experimental results by Huang et al. [11]
states a gain of about 90.8% for the above method with codebooksize of
N = 256 and k = 8 compared to the exhaustive search algorithm. Anyway it
has to be mentioned, that we have an increase in memory complexity due
to the distance matrix, which has a maximal size of N2/2. This
can be annoying when using a codebook with a large size. Therefore the
size of the reference vectors set is often reduced.
2.2.2 Vector-to-Scalar
Mapping Elimination
- In the before discussed triangular inequality elimination method, it
was still necessary to calculate the distortion between pairs of vectors.
To avoid this, a further gain in complexity reduction can be obtained,
when only the criterion ci is used to find the optimal vector.
Li and Salari [16] have showed that such
a vector to scalar mapping elimination method can be derived from the triangular
elimination method, known as mean ordered algorithm, which have been proposed
by Ra and Kim [17] and Poggi [18].
The problem of this method is its ambiguity by mapping a k-dimensional
vector into a scalar, so for two different vectors the same scalar can
be obtained. To avoid this, we can use more than one mapping rule and therefor
more than one criterion to find the optimal vector. Chan and Siu [19]
have proposed such a method with three criterions. An other solution, as
mentioned above, is to find a better criterion than the norm to make an
approximation for the optimal vector and then to search in its neighborhood.
There exists different mapping rules or transformation methods to obtain a better criterion. One of these is the Karhunen-Loeve transformation or principal component analysis. This has been proposed for vector quantization by Chang et al. [20] and Lin and Tai [21] and it will be now discussed.
- The codebook can therefor be regarded as a set of fixed points in a
k-dimensional space. To reduce the dimensionality a projection of the codevectors
on an axis is performed. There the axis is chosen in the direction with
the maximum variance for the mapped values. We make the assumption, that
the mapping preserves the distribution of the source vectors and thus the
scalar values are not correlated. So the covariance matrix for the codebook
is calculated, further its eigenvalues and eigenvectors. The eigenvector
with the corresponding maximal eigenvalue is when the searched direction
also named central line. Guan and Kamel [22]
have showed that it is sufficient to use only the central line as projection
axis. Further they concluded that this axis should follow the principal
axis of the source vectors when a well-trained codebook is used.
So to encode a source vector x we evaluate the projected value px by
- There T is the transformation matrix, here equal to the k-dimensional
eigenvector, the direction of the central line. When we search the codevector
ym
which its projected value pm is closest to px. Further
we compute the distortion between the source vector and the approximate
codevector ym. The optimal codevector is searched in
the neighborhood of ym by alternating choosing a codevector,
which its projected value pn is greater or smaller than pm.
So the first codevector to consider has the projected value pn
= pm+1, the second pn = pm-1, the third
pn = pm+2 and so on until the optimal codevector
is found.
- The bouncing around the approximate codevector is often omitted and
the search range is limited. To avoid suboptimality this window has to
be chosen large enough. The vector-to-scalar mapping elimination method
with a fixed range is also known as hyperplane partitioning method. There
the codevectors lies in planes perpendicular to the central line and the
range is determined by the planes touching a hypersphere who surrounds
the approximated vector. The theory for this method has been elaborated
by Friedman et al. [23] where an overview
is given by Lee and Chen [24].
Like above the variety of vector-to-scalar mapping elimination methods permits only a general description, which can be subdivided in the steps mapping and search. Following this is illustrated by the above-described method.
given
- codevectors yi
there i=1...N
source vector x
precalculation
- - calculate covariance matrix
of codevectors yi
- calculate eigenvectors of covariance matrix
- assign eigenvector with maximum eigenvalue
to transformation matrix T
- determine projected value pi=T×yi for each
codevector yi
- sort codevectors yi by ascending order of pi
mapping
- determine projected value px=T×x for the
source vector x
- identify codevector ym with pm most nearly to px
search
- - determine distortion d2(x,ym)
- search nearest neighbor codevector y in the
neighborhood of ym by alternating computing the
distortions d2(x,yn=m+j)and d2(x,yn=m-j) there
j=1...£ N/2 until codevector y is found
- assign imin= m± j
Complexity
Again in view of the general description the complexity can only be estimated. We have seen that the vector-to-scalar elimination method contributes to the complexity a fix and a variable part. There the fix part includes the mapping and the variable part includes the neighborhood search.
The mapping is a scalar product between two k-dimensional vectors, so we need (k-1) addition and k multiplication to get px. The identification of the approximation vector needs log2(N) comparisons when using a binary search algorithm. For the distortion we need (2k-1) additions and k multiplication when assuming the Euclidean squared vector norm. Further we get 4NMk-NM-k total operations for the neighborhood search using the exhaustive search algorithm. There NM is the average number of affected codevectors, who should be much smaller than the codebook size N. Lin and Tai [21] states an average number of NM = 9.45 ... 22.53 for codebook with N = 512 and k = 16 and NM = 3.53 ... 12.41 for a codebook with N = 256 and k = 16. The following table resumes the above estimations.
| fixed part | variable part | |
| number of additions S per vector | 3k-2 | (2k-1)NM |
| number of multiplication P per vector | 2k | NMk |
| number of comparisons C per vector | log2(N) | NM-1 |
| total | 5k-2+log2(N) | 3NMk-1 |
- The similarity of the triangular inequality elimination and the vector-to-scalar
elimination method is obviously if we compare their total number of operations.
Both have the same structures only differing by the number of comparisons.
So with the results of Lin and Tai [21]
we obtain a computational complexity reduction of about 93.5% ... 97.3%
who is slightly better.