Parâmetros de qualidade de imagens

• Ruído

Em radiografia e tomografia, o ruído pode degradar significativamente a qualidade de uma imagem. A influência do ruído em uma imagem pode ser medida pela relação sinal-ruído (SNR - signal-to-noise ratio). O ruído é geralmente causado pelos seguintes fatores:

• Variação da intensidade da fonte de raios X
• Variação de brilho da imagem de saída do intensificador de imagens
• Variação dos tons de cinza da imagem registrada pela câmera CCD

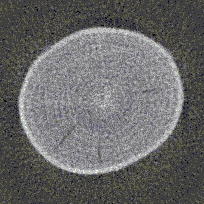
A relação sinal-ruído representa o quanto o ruído prejudica a informação contida em uma imagem. Quanto maior o seu valor, menor a influência prejudicial causada pelo ruído. As figuras abaixo mostram uma imagem com diferentes relações sinal-ruído.

(a)	(b)
(c)	(d)
[Fig. 1] Exemplos de diferentes relações sinal-ruído e suas influências em uma imagem. Observe-se que, em (a), a região clara central é quase indistinguivel.

Uma maneira de reduzir o ruído em uma imagem consiste em tomar a média de um certo número de quadros. Como o ruído é aleatório e com média nula, ao somar os valores dos pixels de uma imagem, o ruído tende a se cancelar. Este método é também conhecido como overlay. A figura 2 apresenta um exemplo de radiografia de um isolador polimérico sem e com redução de ruído. O quadro da esquerda mostra uma imagem capturada por uma câmera CCD. O quadro da direita mostra uma imagem resultante da média de 10 quadros. Observe-se que o quadro da direita apresenta uma menor variação de tons de cinza, ou uma maior relação sinal-ruído.

(a)	(b)
[Fig. 2] Exemplo de redução de ruído por média em uma radiografia de isolador polimérico - (a) Radiografia sem média; (b) Radiografia com média de 10 quadros.




Um outro método de reduzir o ruido em uma imagem consiste em aplicar o filtro da mediana. O filtro da mediana, muito empregado na área de processamento de imagens, apresenta um desempenho superior ao do filtro da média. Para cada pixel de coordenadas (x,y) de uma imagem, a mediana é calculada seguindo as etapas abaixo:

1. Armazenar em um vetor os pixels de uma vizinhança (ou janela) N x N com centro em (x,y).
2. Ordenar o vetor de pixels de forma crescente (ou decrescente).
3. Substituir o pixel (x,y) pelo valor do meio do vetor de pixels ordenados.

A figura 3 ilustra um exemplo de cálculo da mediana para o pixel central da região apresentada. A janela adotada possui tamanho 3 x 3. A matriz superior apresenta os valores originais dos pixels. Os pixels (3,3), (2,4) e (4,4) representam ruído. O vetor da região intermediária apresenta os pixels ordenados em ordem crescente. O valor do meio é substituído no lugar do pixel central, como mostra a matriz inferior esquerda.


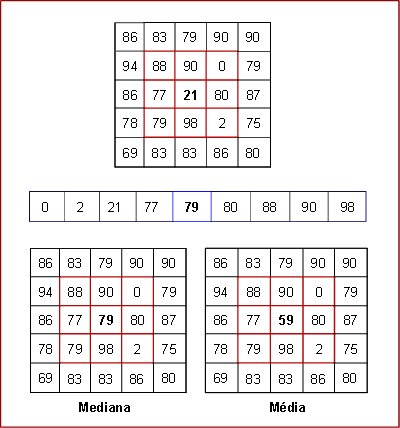
[Fig. 3] Exemplo de aplicação do filtro da mediana.

Desta forma, o efeito do filtro da mediana é o de remover ruído (como no exemplo acima) e de suavizar a imagem. Por descartar os valores extremos em cada vizinhança, a mediana remove ruído de maneira mais eficiente que a média. No exemplo anterior, a média da janela ao redor do pixel central seria 59, um valor não tão proximo ao dos pixels vizinhos.

O filtro da mediana também é superior ao filtro da média com relação às bordas presentes nas imagens. Enquanto a mediana preserva as transições rápidas, a média, por considerar os valores da janela no cálculo do valor final de cada pixel, atenua estas transições. Esta caracteristica é apresentada no exemplo da figura 4:


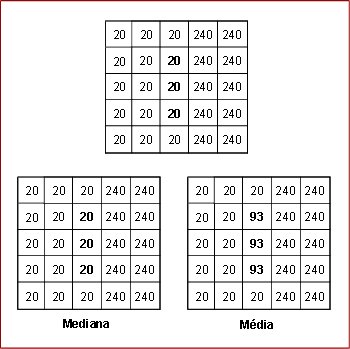
[Fig. 4] Efeito dos filtros da mediana e da média em bordas.

A figura 5 mostra a diferença entre duas tomografias reconstruidas a partir de um conjunto de projeçoes nao filtradas e um conjunto de projeçoes filtradas com o filtro da mediana. Foi utilizada uma janela 5x5. Clique na imagem para ver uma versao mais ampliada.

(a)	(b)
[Fig. 5] Tomografia de uma amostra de madeira (a) sem mediana e (b) com mediana de janela 5x5.



• Contraste



Contraste (ou modulação), calculado pela expressão abaixo, é a diferença de tom entre duas regiões vizinhas de uma imagem.




• C = Contraste
• I₁ = Luminosidade da região mais clara
• I₂ = Luminosidade da região mais escura
• I_max = Maior luminosidade possível (banco total)
• I_min = Menor luminosidade possível (preto total)



Em imagens de 8 bits, I_min vale 0 e I_max vale 255. A figura abaixo apresenta um exemplo de contraste de 100% entre uma região branca e uma região preta. Neste caso, I₁=255 e I₂=0.


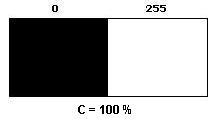
[Fig. 3] Exemplo de contraste de 100%

À medida em que a diferença de tom entre as duas regiões é reduzida, o valor do contraste também diminui. Quanto menor o contraste, mais difícil torna-se diferenciar as regiões vizinhas.


[Fig. 4] Exemplo de contraste de 49,8%

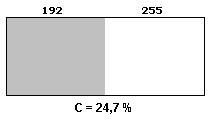
[Fig. 5] Exemplo de contraste de 24,7%

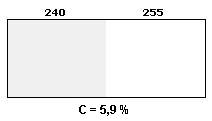
[Fig. 6] Exemplo de contraste de 5,9%


• Resolução



A resolução de um dispositivo ou sistema representa sua capacidade de apresentar fielmente pequenos detalhes ou variações de uma imagem. A resolução pode ser expressa em diversas unidades: pixels/mm, pixels/polegada, pares de linha/mm, etc. Existem dois tipos de resolução: resolução de alto contraste e resolução de baixo contraste.

• Resolução de alto contraste



A resolução de alto contraste representa a capacidade de um sistema de apresentar fielmente imagens com grandes variações de intensidades. Um método comumente empregado para determinar a resolução de alto contraste de um dispositivo consiste em observar a imagem de uma sequência de linhas escuras e claras alternadas (de forma a produzir altos valores de contraste), como mostra a figura abaixo.


[Fig. 7] Padrão para medição de resolução

Os primeiros pares de linhas são facilmente distinguíveis. Ao caminhar para a direita, os pares de linha tornam-se cada vez mais próximos. Em outras palavras, a frequência espacial da imagem (o número de pares de linha por unidade de comprimento) aumenta. Como consequência, torna-se mais difícil distinguir uma linha escura de uma outra linha escura vizinha. Neste método, a resolução é geralmente expressa em pares de linha/mm.

Em radiografia, este método pode ser realizado utilizando um padrão com diversos fios de cobre de diferentes diâmetros. Em cada sequência, os fios de cobre devem ser espaçados por uma distância igual ao seu diâmetro.


[Fig. 8] Padrão para determinação de
resolução em radiografia e tomografia

Desta forma, a imagem formada pelo sistema assemelha-se ao padrão de linhas claras e escuras apresentado acima. Usando fios cada vez mais finos e reduzindo o espaçamento entre eles, é possível determinar a resolução máxima do sistema.


[Fig. 9] Radiografia do padrão de resolução mostrado acima



Uma forma eficiente de observar uma radiografia e verificar seu limite de resolução em alto contraste consiste em analisar o perfil de luminosidade das sequências do padrão de alto contraste. A imagem a seguir apresenta o perfil referente ao padrão de resolução de alto contraste acima.


[Fig. 10] Perfil de luminosidade de padrão de resolução de alto contraste



Nota-se que quanto maior a resolução espacial, menor a diferença entre os máximos e os mínimos do perfil de níveis de cinza. O limite máximo da resolução pode ser encontrado quando a diferença percentual entre o máximo e o mínimo cai abaixo de um determinado valor.

Em tomografia, a resolução de alto contraste de um sistema pode ser encontrada utilizando um corpo de prova com vários furos de diversos diâmetros. Realizam-se assim tomografias do corpo de prova, e observa-se o menor furo distinguível na tomografia. A figura 11 mostra uma fotografia de um corpo de prova de acrílico (a) e uma tomografia do corpo de prova (b).

(a)	(b)
[Fig. 11] Fotografia (a) e tomografia (b) de um corpo de prova de acrílico.



• Resolução de baixo contraste



A resolução de baixo contraste representa a capacidade de um sistema de apresentar detalhes com pequenas variações de intensidades. Em radiografia e tomografia, este parâmetro é a capacidade de mostrar pequenas variações de coeficientes de atenuação. A resolução de baixo contraste deve ser expressa em termos do tamanho do menor detalhe e do contraste em relação ao meio (por exemplo, 1 mm a 1%).

Um método comum para determinar a resolução de baixo contraste de um tomógrafo consiste em utilizar um phantom cilíndrico de acrílico com diversos furos de diferentes diâmetros. Os furos devem ser preenchidos com líquidos de coeficientes de atenuação próximos ao coeficiente do acrílico, como glicerina. O menor furo distinguível fornece a resolução de baixo contraste.

(a)	(b)
[Fig. 12] (a) Phantom para determinação de resolução de baixo contraste (b) Seção interna do padrão

A figura abaixo mostra uma radiografia de um isolador de polietileno que rompeu. O isolador apresenta uma trinca entre a rosca central e a parte externa. Vista de frente, esta trinca aparece como uma linha mais clara, devido à menor atenuação dos raios-X que atravessam seu interior.


[Fig. 13] Radiografia de um isolador de polietileno rompido.
A trinca (linha clara no centro) está perpendicular ao plano da figura.

Por outro lado, ao rotacionar o isolador 90 graus, os raios-X que atravessam a trinca sofrem praticamente a mesma atenuação que aqueles que atravessam o polietileno vizinho. Assim, não é possível distinguir o caminho de ruptura com o isolador nesta posição.

Um meio de contraste pode ser utilizado para tornar o caminho de ruptura do isolador visível. Em radiologia médica, meios de contraste, como soluções de bário ou de iodo, são comumente empregados. A figura a seguir mostra uma radiografia do isolador acima preenchido com uma solução de sulfato de bário. Como o bário é um elemento de peso atômico elevado, a alta atenuação causada pela solução dentro do isolador proporciona um contraste maior entre a trinca e o polietileno vizinho. Agora é possível visualizar o pequeno caminho de ruptura entre a cavidade à esquerda (originada pelo pino no interior na rosca) e o exterior do isolador.


[Fig. 14] Radiografia de um isolador rompido preenchido
com uma solução de sulfato de bário.


• Função de Transferência de Modulação



Resolução e contraste estão interrelacionados. Resoluções altas resultam em baixos valores de contraste, uma vez que o dispositivo produz imagens com transições cada vez menos definidas. Por outro lado, baixas resoluções resultam em altos valores de contraste, já que as transições ocorrem em frequências espaciais menores. Acima de uma determinada resolução, o contraste cai abaixo de um valor mínimo, tornando impossível distinguir pequenos detalhes.

Este comportamento - a dependência do contraste com a resolução - é expresso pela Função de Transferência de Modulação (MTF - Modulation Transfer Function). Em fotografia, por exemplo, cada componente de uma máquina fotográfica possui uma MTF. A resposta final do dispositivo é o resultado das MTFs de todos os seus componentes.