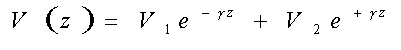--- ( 11 )Actualizada: mayo, 2004
Las ecuaciones 9 y 10, son las ecuaciones diferenciales que controlan las distribuciones de tensión y corriente a lo largo de la LT. Las soluciones de éstas son:
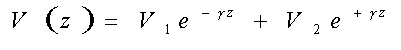--- ( 11 )
--- ( 12 )En las ecuaciones anteriores, V(z) e I(z) son respectivamente el fasor de tensión y el fasor de corriente en cualquier coordenada z de la línea. Los términos V1, V2, I1 e I2 son también fasores.
Ejemplo: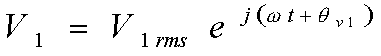
Nota: Las magnitudes fasoriales de tensión o de corriente, es decir, en forma polar, siempre deben indicar valores rms. No se volverán a definir mediante subíndices en estos apuntes.
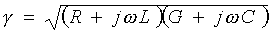--- ( 13 )Como se observa, el resultado será una cantidad compleja, la cual se expresa como:
Así entonces, separando partes real e imaginaria del factor de propagación y a partir del ejemplo anterior, el primer término de la ecuación para la tensión (11) implica lo siguiente:
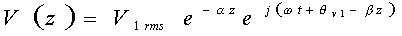
En una posición seleccionada z1 sobre la línea, en un instante escogido t1, la tensión representada por el primer término de la ec. (11), tiene una fase representada por (wt1 -bz1+ q). En un instante ligeramente posterior t1+ Dt, el valor de la fase mencionada habrá cambiado en el punto z1, pero el valor original se encontrará en una posición ligeramente diferente sobre la línea z1+ Dz, tal que:
w
(t1+ Dt) - b(z1+ Dz ) + q = wt1 -bz1+ qLuego:
w D
t - b Dz = 0De aquí:
D
z / Dt = w / bSe observa que un punto de cierto valor de fase del patrón de tensión avanza hacia valores superiores de z a medida que el tiempo aumenta, obedeciendo la relación anterior.
En el límite cuando
Dt =0 se tendrá dz/dt = w / b, y esta relación es denominada velocidad de fase pues esta es la velocidad a la cual un punto de valor de fase constante avanza a lo largo de la línea de transmisión. Luego entonces:vp
= w / b --- (14) FACTOR DE FASE (b ) .-El término e-j
bz es un número complejo cuya magnitud es la unidad y cuyo ángulo de fase es bz radianes. No afecta a la magnitud de los fasores de tensión o corriente. Solo afecta a la fase, disminuyéndola en la dirección de incremento de z.La longitud de onda l es la distancia entre puntos sucesivos de la onda con la misma fase eléctrica. De acuerdo a lo expuesto, la fase original de la onda incidente es (wt + q ), y es modificada en la medida que la onda avanza, en un factor bz radianes, esto es: (wt - bz + q ).
Así entonces, bz será igual a 2p radianes si la distancia z es igual a l . O sea:
Al reducirse la vp, la longitud de onda en la línea se reduce también en forma proporcional. En las LT (modo TEM), la velocidad de propagación sería igual a la velocidad de la luz si el dieléctrico entre los conductores fuera aire, pero si el medio tiene una constante dieléctrica relativa er mayor que la unidad, la velocidad de propagación será menor, e igual a :
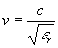--- (16)Nota: El término que multiplica a la velocidad de la luz es denominado factor de velocidad (k), y se expresa como un porcentaje.
La velocidad de fase y la velocidad de propagación son numéricamente iguales en las LT (modo TEM). Para un medio sin pérdidas se puede considerar entonces que:
--- (17)donde l
0 = longitud de onda en el espacio
libre a la misma frecuencia.
El tiempo que tarda la onda en avanzar la longitud total de la línea es llamado tiempo de retardo de la línea (td), y es igual a:
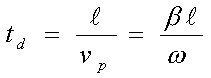--- ( 18 )Ejercicio 1 .- En una LT de radiofrecuencia, la velocidad de las señales a una frecuencia de 125 MHz es de 2.1 x 108 m/seg. ¿Cuál es la l de la señal y cuál es el factor de fase b a esa frecuencia?
Ejercicio 2 .- En una LT, el factor de fase es de 0.123 rad/metro a una frec de 4.5 MHz. La longitud de la línea es de 500 metros. Encuentre su longitud de onda y la velocidad de fase, la diferencia de fase entre los fasores de tensión en los dos extremos de la línea y el tiempo requerido para que un punto de referencia sobre el patrón de la señal avance la longitud total de la línea.
Una onda de tensión o corriente experimenta una atenuación de N néper cuando su magnitud cambia en un factor e -N a medida que la onda avanza entre dos puntos en una línea de transmisión. El valor en Nepers se puede cambiar a dB mediante la relación:
Ejercicio 3.- ¿En qué factor disminuye la magnitud del fasor de tensión si experimenta una atenuación de 3 Nepers?
Resolución:Ejercicio 4.- Si una onda de corriente sufre una reducción en magnitud en un factor de 10 al avanzar una longitud particular de línea de tx, ¿Cuál es la atenuación de esa sección de línea en Nepers? Exprese también en dB.
Resolución:
e - N = 1 / 10
...
Ejercicio 5.- Se transmite potencia eléctrica a una cierta frecuencia desde una fuente a una carga por una LT uniforme de 500 metros de longitud, sin ondas reflejadas. La tensión de entrada es de 250 Volt rms, y en la carga se miden solo 220 Volts rms.
¿Cuál es la atenuación total de la línea y cuál es el factor a para esta LT?
Ejercicio 6.- Una línea telefónica tiene una atenuación de 1.5 x 10-4 nepers/metro a una frecuencia de 1000 Hz. Dicha línea tiene una longitud de 50 Km. Si la corriente de entrada a la es de 650 mA a la frecuencia dada, ¿Cuál será la corriente en la carga, suponiendo que en la línea no se presentan ondas reflejadas?
En una línea de tx uniforme sin ondas reflejadas, la relación fasorial V / I se mantiene uniforme en todos los puntos de la LT, ya que los términos e-az y e-jbz son idénticos para ambos.
Esta relación es una cantidad compleja determinada por los coeficientes de circuito distribuido de la línea y la frecuencia de la señal; debido a esto y a que la relación V/I tiene dimensiones de impedancia, se le denomina "impedancia característica" de la línea (Z0) y está dada por:
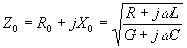--- ( 19 )
La impedancia característica no "existe" en la línea en un sentido simple y obvio, es decir, no se puede medir directamente con un puente de impedancias sobre una longitud única y arbitraria.
Se puede calcular a partir de la medición de los coeficientes de circuito distribuidos y sustituyendo valores en la ec. 19. Esta es una de las prácticas en el laboratorio.
También se puede determinar experimentalmente midiendo la impedancia de entrada de la línea bajo dos condiciones: con en el extremo terminal en corto circuito (Zsc) y en circuito abierto (Zoc). Con estos datos:
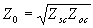--- (20)Esta es una ecuación universal y muy útil para obtener la impedancia característica de cualquier tipo de línea, a partir de dos medidas de impedancia hechas sobre una muestra de longitud de línea, usando dos terminales de carga que son fácilmente disponibles (abierto y corto circuito). Aunque se deben hacer dos consideraciones:
El medidor debe poder hacer mediciones de impedancias balanceadas o desbalanceadas. Las primeras se refieren a conductores simétricos (línea de alambres paralelos o par blindado); las segundas a líneas con un conductor a "tierra" o como blindaje (línea de banda o un coaxial).
Segundo.- La longitud de la línea no puede ser completamente arbitraria. Si la línea es muy corta, Zsc puede ser muy pequeña y Zoc demasiado grande para que puedan ser medidas con exactitud por cualquier puente disponible. La longitud de línea especialmente útil para estos casos debe ser comparable con cualquier múltiplo impar de octavos de longitud de onda ( l / 8); para tales longitudes, las impedancias característica, impedancia en corto e impedancia en circuito abierto tendrán magnitudes similares. Si la l se conoce solo con aproximación, las medidas se pueden hacer para diferentes valores de l hasta lograr encontrar esta condición.
Ejercicio 7.- Una LT coaxial se usa a una frecuencia de 100 MHz y tiene los siguientes coeficientes de circuito distribuido:
R = 0.098 W/m, L = 0.32 x 10 - 6 H/m, G = 1.5 x 10 - 6 S/m, C = 34.5 x 10 - 12 F/m
Encuentre la Z0 a la frecuencia de operación y el Factor de Propagación.
Resolución:LÍNEA ACOPLADA.-
En una línea infinita no habrá reflexión. Una onda incidente siempre "verá" hacia la terminal de carga una impedancia Z0, independientemente de la coordenada z en la que se encuentre.
Se puede pensar entonces que si al final de una línea finita de impedancia Z0 se coloca una carga terminal ZT igual a Z0 , la línea se comportará como infinita y no habrá reflexiones. Toda la potencia incidente se proporcionará entonces a la carga. Cuando esto sucede se dice que la línea está acoplada.
En conclusión:
1.- El valor de la impedancia de carga terminal ZT que se debe conectar para evitar ondas reflejadas debe ser igual a la Z0 de la LT.
2.- La impedancia de entrada de cualquier longitud de LT uniforme terminada en la Z0 (sin reflexiones), es igual a la Z0 de la LT.
Ejercicio 8.- Una LT de alambres paralelos tiene una Z0 de 700 -j 150 W a una frecuencia de 8 KHz. La ZT de carga conectada a la línea es igual a la Z0 . Si una tensión de la señal de 10 Volts rms a 8 KHz se conecta a las terminales de entrada de la línea, ¿Cuál es la corriente de entrada y cuál es la potencia real suministrada por la fuente de señal a la línea?
Las líneas de tx disponibles comercialmente se indican con ciertos valores tales como 50 o 75 Ohms, implicando un valor puramente resistivo y además independiente de la frecuencia.
Esto no está obviamente de acuerdo con la ec. (19). La explicación es que para la mayoría de las LT prácticas, los valores de R, L, G y C son tales que, a medida que la frecuencia aumenta, la Z0 alcanza un valor aproximadamente constante, y su ángulo de fase se vuelve despreciable.
Si las relaciones wL/R y wC/G son suficientemente grandes comparadas con la unidad, las expresiones siguientes pueden sustituir a las correspondientes:
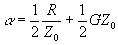--- ( 21 )
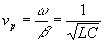--- ( 22 )
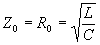--- ( 23 )X0 = 0
Las expresiones anteriores son conocidas como "aproximaciones en altas frecuencias". En general, estas expresiones son suficientemente exactas para propósitos prácticos si wL/R y wC/G son mayores que 10, y proporcionan cálculos bastante buenos si son mayores que 5. Normalmente wC/G es mucho mayor que wL/R, por lo que será suficiente probar el valor de esta última relación.
Ejercicio 9.- Observar si es posible aplicar las expresiones anteriores en el ejercicio 7 y comprobar los resultados para Z0, a y b.
w
L/R = ...Ejercicio 10.- Un generador de señales está conectado a una LT cuya impedancia característica vale 75 W. La línea mide 6 metros y el dieléctrico en su interior tiene una permitividad relativa de 2.6. Al final de la línea se conecta una carga cuya impedancia de entrada vale 75 W. Si el generador tiene una resistencia interna de 1 W y una tensión de salida en circuito abierto igual a 1.5 cos( 2 p x 10 8 t ) Volts, encuentre:
a).- Las expresiones matemáticas instantáneas para la tensión y la corriente en cualquier punto de la línea.
b).- La potencia promedio que se le entrega a la carga.