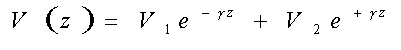V₁ + V₂ = V _in, es la tensión fasorial en las terminales de entrada de la línea. Este comportamiento se aplica idénticamente a ondas de corriente.

Existirán ondas reflejadas si en el extremo de la línea (z = l), la impedancia terminal de carga Z_T requiere relaciones de magnitud y fase entre la tensión y la corriente, diferentes de las relaciones que existen para las ondas que llegan. Los valores fasoriales de las ondas reflejadas serán tales que cuando éstas se combinan con los valores fasoriales de las ondas incidentes, se satisfacen las condiciones de borde en la terminación, impuestas por la impedancia Z_T.
Cuando una línea termina en una impedancia Z_T distinta de Z₀ habrá siempre ondas reflejadas y la impedancia en cualquier punto de la línea diferirá de Z₀.

Se define como la impedancia de entrada de la sección de línea del lado de la carga terminal del punto, cuando la porción de línea del lado del generador se ha eliminado.

Sabemos que:

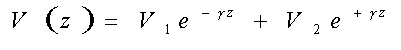----- (11)

Derivando:

Y también, (ec. 7)

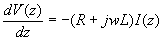----- (7)

Igualando y despejando I(z):

Por lo tanto:

-----( 24 )

La Z en cualquier punto de la línea será la razón entre la tensión ec ( 11 ) y la corriente ec ( 24 ).
En el extremo terminal (z = l ), esta relación será igual a la Z_T. Esto implica:

-----( 25 )

El término V₂ e ^+gl representa el valor fasorial en z = l , de una onda reflejada que avanza en dirección decreciente de Z. Esta reflexión es función de la impedancia Z_T.

Coeficiente de Reflexión (r_T) .-

Se define como el cociente del valor fasorial de la tensión reflejada y el valor fasorial de la tensión incidente, en el punto de reflexión, esto es, en la carga terminal.

Así entonces:

-----( 26 )

Dividiendo los términos de la derecha de ( 25 ) entre V₁ e^-gl se obtiene:

-----( 27 )

La relación Z_T / Z₀ se denomina valor normalizado de Z_T, y es el valor utilizado en los cálculos mediante la Carta de Smith.

El Coeficiente de Reflexión en función de la Z_T normalizada es:

----- ( 28 )

Razón de Onda Estacionaria de Tensión (ROE) .-

En inglés: Voltage Standing Wave Ratio (VSWR); se define como la relación entre la magnitud máxima de la tensión a la magnitud mínima, en referencia a la onda estacionaria de la tensión.

Esto es: ROE = | V _max | / | V _min |

En función del Coeficiente de Reflexión: ----- ( 29 )

Como r_T tendrá valores entre cero y uno, la ROE los tendrá entre 1 e ¥ . La ROE es función de la magnitud del Coeficiente de Reflexión, mientras que la localización de los máximos y mínimos de tensión son función del ángulo de fase de dicho coeficiente.

Ejercicio 1.-

Una LT con una Z₀ de 50 + j 0 Ohms, está terminada en una impedancia de carga de 25 – j 75 Ohms. ¿Cuál es el coeficiente de reflexión de las ondas de tensión en la terminal de carga de la línea? Encuentre también la ROE.

Resolución.-

De la ec.( 28 ):

De la ecuación (29) :

Ejercicio 2.-

Con los datos del ejemplo anterior encuentre el valor normalizado de la impedancia terminal y encuentre el coeficiente de reflexión.

Resolución:
La impedancia normalizada es:
De ( 28 ):
, como anteriormente.

Resolver ahora utilizando Carta de Smith, empleando el valor de Z_T normalizada.

Ejercicio 3.-

El coeficiente de reflexión producido por una impedancia terminal es de – 0.65 + j 0.25. La impedancia característica es de 52 + j 0 Ohms. Encuentre el valor de la impedancia de carga.

De la ec ( 27 ):



Resolver mediante Carta de Smith:

r = -0.65 +j 0.25 = 0.696 Ð158.96° ; aprox=0.7 Ð159° . Al graficar se obtiene una Z_T normalizada de 0.18 + j 0.18 Ohms.......

Impedancia de entrada de una LT.-

De las ecuaciones (11) y (24), la impedancia de entrada en cualquier punto se expresa mediante:

Dividiendo numerador y denominador entre V₁, sustituyendo después r e ^{-2 g l} = V₂ / V₁ y multiplicando después por e^{g l} / e^{g l} , se obtiene la siguiente expresión para la impedancia de entrada en cualquier coordenada de la LT medida desde la terminal de carga:

----- (30)
Sustituyendo r de la ec.(28) se obtiene:

Aplicando las identidades:

; se tiene:
----- (31)

O también:

----- (32)

La impedancia de entrada se encuentra en una coordenada d medida desde la terminal de carga, así entonces cualquiera de las expresiones anteriores (30), (31) y (32), expresará la Z_in normalizada si la coordenada d se sustituye por l . Así entonces, de la ec (32) se tiene:

----- ( 33 )

La expresión anterior determina entonces la Impedancia de entrada normalizada de una línea de transmisión de cualquier longitud l.

Determinación de la Impedancia Característica a partir de las mediciones de Z_sc y Z_oc.-

A partir de la ecuación anterior, se puede determinar la impedancia de entrada para los casos de terminación en corto y circuito abierto, de la siguiente manera:

Con terminación en corto circuito, es decir Z_T = 0, se tendrá:

Si ahora se terminara en circuito abierto con Z_T = infinito, la ecuación quedaría:

Si ambas impedancias se miden a la misma frecuencia, entonces Z₀, a, b y l tendrán los mismos valores en ambas ecuaciones. Multiplicando ambas: Z_sc Z_oc = Z₀²

Esto es: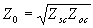 --- (20)

Como se había expresado anteriormente en la parte 2 de estos apuntes. A continuación veremos otra aplicación interesante de la misma expresión.

Determinación del Factor de Propagación a partir de las mediciones de Z_sc y Z_oc.-

Al dividir las expresiones correspondientes a Z_sc y Z_oc se tiene:

y como:

se obtiene:

de aquí tenemos:

y finalmente despejando g mediante logaritmo natural:
----- ( 34 )

Así se obtiene el factor de propagación a partir de lecturas de impedancias en corto y circuito abierto. Se tiene cierta complicación para el cálculo del factor de fase, como se verá en el ejemplo siguiente.

Ejercicio 4.-

A 20 MHz, la impedancia de entrada de una sección de LT coaxial flexible de 32 mts. se ha medido terminada en corto y en circuito abierto, obteniendo los siguientes valores: Z_sc = 17 + j 19.4 W , y Z_oc = 115 – j 138 W . Encuentre la Z₀, el factor de atenuación y el factor de fase.

Resolución:

Considerando que:ln A e ^jq = ln A + j (q +2np )

El coeficiente de atenuación es igual a:

a = 7.195 x 10^-3 Néper/metro.

El coeficiente de fase es igual a:

Así entonces, de acuerdo a la ecuación anterior, tenemos varios valores posibles para b, como se indican en la siguiente tabla para distintos valores de n.

Podemos descartar algunos valores considerando que b = 2p/l. Aunque no se conoce la longitud de onda en la línea, a partir de la longitud de onda en el espacio libre se puede hacer una estimación para b :

l₀ = c / f = 3 x 10⁸ / 20 x 10⁶ = 15 metros.

Y como l < l₀ , el valor de b debe ser mayor que 0.418 rad/metro. De esta forma se descartan los valores de n desde 0 hasta 4. Ahora bien, considerando una longitud de onda de la línea entre un 30 y 50 % menores a l₀, se tendrían valores entre 0.545 y 0.6285 para b.

El valor de 2.704 (y mayores) para b no son factibles pues el primero implicaría una longitud de onda de 2.327 metros, con una velocidad de fase de solamente el 15.5% de la velocidad de la luz. Así entonces el único valor posible de esta tabla es el de b = 0.61; el valor correspondiente más cercano que se observa de la primera tabla es b = 0.598, que es el valor correcto, para n = 6.

En este caso, l = 10.5 metros y v_p = 2.1 x 10⁸ metros/seg.

De la ecuación (20), para una línea de longitud l terminada en corto circuito (Z_T = 0) y con atenuación despreciable (a = 0) se tiene:

----- (35)

Similarmente para la misma línea, pero con una terminación en circuito abierto (Z_T = ¥ ):

----- (36)

Normalmente Z₀ es una resistencia pura, por lo tanto de las ecuaciones anteriores se puede observar que las impedancias de entrada de secciones de línea de baja pérdida, con terminaciones en corto o en circuito abierto, son reactancias puras.

Esto se observa en la siguiente tabla para distintos valores de l , partiendo de la ec. (35), para una línea terminada en corto.

Para longitudes de línea cortas (atenuación despreciable) entre cero y l/4 y con terminación en corto circuito se tendrán valores correspondientes a un inductor, como se deduce de la tabla anterior, y se observa en la siguiente gráfica de la función tangente.

A frecuencias de cientos de MHz, una longitud de onda se convierte en una longitud física suficientemente pequeña, la cual puede ser incorporada en equipos. La atenuación de tales secciones de línea es muy pequeña (a << b). Estas secciones de línea pueden contribuir con sus capacitancias e inductancias como si fueran componentes de circuito, para adaptar impedancias y se conocen como líneas "STUB"

Se requiere calcular b = 11.22 rad/metro.

Como se trata de una línea terminada en circuito abierto, se utiliza la ecuación 36, de donde se despeja l , la cual es igual a: l = 0.0926 metros + n l/2. La distancia más corta será entonces de 0.0926 metros.

Respuesta: El desplazamiento correspondiente es de 0.182l. La suceptancia será de 0.75 positiva (capacitor).

Respuesta: Admitancia Terminal Normalizada = 0.577 – j 0.3846. A un desplazamiento de d = 0.232l se encuentra una Admitancia Normalizada = 1 + j 0.75 Siemens. La longitud del stub terminado en corto circuito (Admitancia Infinita), con valor de – j 0.75, es de l = 0.148l.