Kapitel 4
Die Beziehungen zwischen den trigonometrischen Funktionen
Die trigonometrischen Funktionen
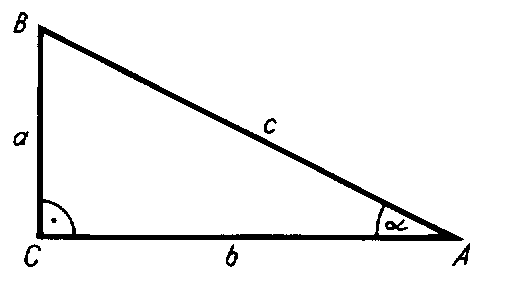
Sie haben im vorigen Kapitel gesehen, daß die
Seitenverhältnisse in einem rechtwinkligen Dreieck eindeutig bestimmt sind, wenn einer
der beiden spitzen Winkel bekannt ist. Für drei dieser Verhältnisse haben wir die
Bezeichnungen Sinus, Kosinus und Tangens eingeführt:
| Gegenkathete a sin  =
---------------------- = --- Hypothenuse c Ankathete b cos
= ----------------- = --- Hypothenuse c
Gegenkathete
a |
 |
Für jedes rechtwinklige Dreieck gilt: Der Wert der Seitenverhältnisse hängt nur von
der Größe des Winkels ab.
Sie werden sich erinnern, daß man die Abhängigkeit eines
Wertes von einem anderen in der Mathematik eine Funktion nennt. Die drei
Seitenverhältnisse a/c, b/c und a/b sind also im rechtwinkligen Dreieck Funktionen des
Winkels , sie heißen
"trigonometrische Funktionen".
Sie sollten sich jetzt überlegen, ob auch umgekehrt der
Winkel eine eindeutige Funktion
eines Seitenverhältnisses ist. Dann können Sie nämlich die Winkel im rechtwinkligen
Dreieck berechnen, wenn Ihnen die Seiten bekannt sind. Sie wissen zum Beispiel, daß sin
30° = 0, 5 ist. Gibt es noch einen anderen Winkel zwischen 0° und 90°, dessen Sinus auch den Wert 0, 5
hat?