Sie haben recht: man kann gleichseitige Dreiecke von verschiedener Seitenlänge
zeichnen, deren Winkel gleich sind.
Es gibt keine Winkelfunktion, durch die eine Dreiechsseite berechnet werden könnte,
wenn nur Winkel bekannt sind. Das ist verständlich, denn die Seiten eines Dreiecks sind
nicht allein von den Winkeln abhängig.
Will man irgendwelche Teile eines allgemeinen Dreiecks berechnen, so müssen drei
Stücke, darunter mindestens eine Seite bekannt sein. Durch Angabe der Winkel
allein ist ein Dreieck nicht bestimmt.
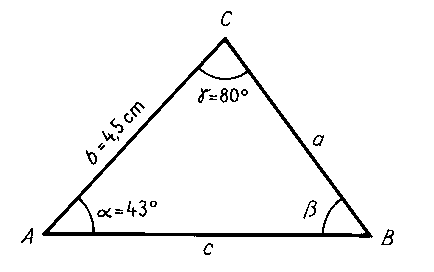
Sie werden nun sehen, wie man ein allgemeines Dreieck, in dem mindestens eine Seite
bekannt ist, berechnen kann. Gehen sie bitte von folgendem Beispiel aus: Im Dreieck ABC
seien gegeben.
b = 4,5cm
![]() = 43°
= 43°
![]() = 80°
= 80°
Schreiben sie sich diese Werte auf, und und zeichen Sie das Dreieck in wahrer Größe. Sie erkennen, daß das Dreieck keinen rechten Winkel enthält und daß Sie daher zur Berechnung irgendeines unbekannten Teiles nicht ohne weiteres eine Winkelfunktion anwenden können. Wenn sie aber jetzt vom Punkt C aus ein Lot auf die gegenüberliegende Seite c fällen, so zerlegen Sie damit das Dreieck in zwei rechtwinklige Teildreiecke. Dieses Lot nennt man die "Höhe h" des Dreiecks.
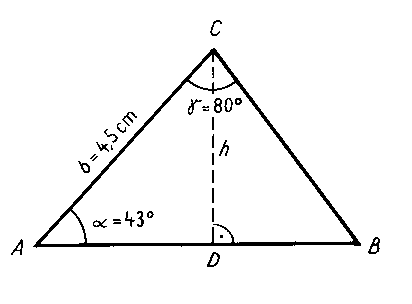
Sehen sie den Weg, auf dem es gelingt, nun die Seite c = AB zu berechnen?