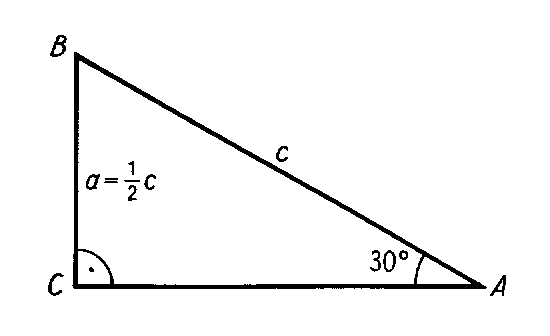
Sie haben im Kapitel 2 gelernt, daß im rechtwinkligen Dreieck die Gegenkathete eines 30°-Winkels (dies ist die kürzere der beiden Katheten) halb so lang ist wie die Hypotenuse. Daher kann man leicht die Länge der kürzeren Kathete berechnen, wenn die Länge der Hypotenuse gegeben ist. Umgekehrt lässt sich ebenso leicht die Hypotenuse berechnen, wenn die Länge der kürzeren Kathete bekannt ist. Entsprechende Beispiele haben Sie in den letzten Übungsaufgaben gerechnet.

So einfach und selbstverständlich diese Erkenntnis erscheint, so wichtig ist sie für die Seitenverhältnisse in einem rechtwinkligen Dreieck. Sie werden in diesem Kapitel sehen, welche Bedeutung solche Seitenverhältnisse haben.

Betrachten Sie bitte diese Zeichnung:

Die Gegenkathete des 30°-Winkels ist (wie Sie wissen) halb so lang wie die Hypotenuse. Sind nun alle folgenden Gleichungen richtige Aussagen über dieses Verältnis, oder ist eine Gleichung falsch?
Überlegen Sie bitte sorgfältig.
                                                                                             a
(1)    a                            (2)    a = 0,5 c                (3)    c =  ---
       --- = 0,5                                                                       0,5
        c

(4)    a         5                 (5)    a       0,5                (6)    c        1
       --- =   ---                       --- =  ---                        --- =  ---
        c        10                         c       1                           a       0,5

                    Alle Aussagen sind richtig:
                    Mindestens eine Aussage ist falsch: