[Contents Page] [Previous section] [Next section] Back to my homepage
Sections:
3.1 Introduction to Barnett et al.
3.2 The rate equations
3.3 Mathematical analogies
3.4 The Barnett curve
There are various motives for citing previous academic work.[63] Barnett, Fink, and Debus generalize the opposing pressures to cite older or newer material, and model these forces mathematically.
Scholars exhibit two sets of motives by citing others. First, they indicate familiarity with classics in the field ... which tend to be highly cited ... Second, they wish ... to incorporate new theoretical advances, technologies, and research findings in[to] their own work. In addition, scholars value being "up" on the latest literature to convey the idea that they are active and knowledgeable ... The first motive encourages citations to older papers, whereas the latter motives encourage citation to the most recent material. The citation pattern in a given academic area exhibits the relative strength of these two motives.[64]
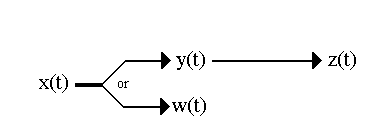
Barnett distinguishes four time-dependent "pools" of published articles:[65]
The flow, or diffusion, of articles is thus:

Disadoption of reference sources in any field is a time-dependent decaying exponential function,[66] i.e., of the generic form dy/dt = -k.y(t) where k>0. The innovation of Barnett et al. is to assume that the flow from pool x(t) --- i.e., the infusion, or absorption, into pools y(t) and w(t) --- is also an exponential function of time. Colloquially, we may say that:
Expression of both the inward and outward flows is a major strength of the model of Barnett, Fink, and Debus; however, their model is not unique. There are analogous patterns in the wider, non-bibliometric world which may also be described by the x(t) ---> y(t) ---> z(t) flow and rate equations of the generic form
dx/dt = -k1.x(t) and dy/dt = k2.x(t) - k3.y(t) where k1, k2, k3 > 0.
From such differential or rate equations, we may obtain (by integration) an equation like that of Barnett et al. for y(t) itself.[67]
Many time-dependent functions are exponential,[68] also termed "first order."[69] By concatenating two appropriate first order processes we may mimic our bibliometric model. Indeed Barnett et al. specifically mention that their model is similar to one that describes the concentration of a drug in the blood.[70] Similarly, the Barnett model's conceptual "pool," y(t), acts like a biological "compartment."[71]
Since one decaying exponential function is the transfer of freely diffusible molecules across a biological membrane,[72] it is understandable that some (by no means all) organs do function as compartments. However it is the existence of measurable rates of change which defines the compartment, not gross or physical structures. [73]
Example 1:

The form
B=A(exp(-ke.t) - exp(-ka.t))
represents absorption into and elimination from a single compartment by first order [i.e., exponential] processes, from a single depot. ... It is often used to describe the behavior of a compound administered orally or from a deposit on the surface of the skin and eliminated by a first order process.[74]
Here: ka = the absorption rate constant, and ke = the elimination rate constant.
Example 2: Ruminant digestion.
It had been established that there is a continuous flow of material from the rumen to the abomasum, and from the abomasum to the duodenum.[75] From known weights, textures, and times of feeding, and the ensuing series of faeces, Blaxter et al. proposed and supported the model [76]
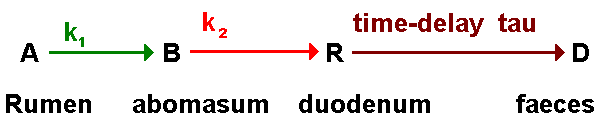
with the rates:
dA/dt = - k1.A and dB/dt = + k1.A - k2.B and dR/dt = k2.B(t-tau)
Although Blaxter et al. were concerned primarily with R(t), we may readily observe that A(t) and B(t) behave like Barnett's pools x(t) and y(t) --- i.e.,
A(t)= A0.exp(-k1.t) and B(t) = ((A0.k1)/(k2 - k1)).(exp(-k1.t) - exp(-k2.t))
The elegant point of this example is that B(t) is never measured. It is a mathematical "black-box" used to produce R(t). [77]
Actually the bibliographic model has the same mathematical principles as ruminant digestion although we have reversed the ease of measurability. For sheep A(t) and D(t), hence R(t), are readily evaluated --- but B(t) is an internal function. For citations we do not know, and cannot measure, the pool of unripe articles in a discipline or subject. Even though many items of a particular x(t) may come from, say, the contents of a core collection of journals, there will be citations from outside those opera: "it is almost impossible to count a total population in any citation context."[78] Even the function x(t)-w(t) is only deducible in vague quantities after the event. Similarly z(t), the pool of exhausted citations, may never be known, although we may approximate its volume if y(t) is known.
Conversely y(t) may be proportionally measured by sampling a suitable selection of citations. In considering pool y(t), we are dealing with the growth and eventual obsolescence of various citation sources as a function of increasing time. By establishing the citation ages of sources used by a suitable sample of a particular body of literature, we are quantifying what Egghe et al. term the synchronous utilization rate,[79] as a function of citation age, which is in fact y(t).[80]
Actually we must emend the formulae of examples 1 and 2 above, because one
may cite articles before they are published.[81] Let
us call this modified pattern, shown in Figure-1,[82]
namely y(t) = a.(exp(d - b.t) -
exp(-c.t)) a Barnett curve, where
t = citation-age [83]
y(t) = calculated relative frequency of
citations, as a function of t,
for all 0 =< t =< 50
where t is an element of
the set {Whole numbers}
Ymax = the maximum value of y(0), y(1), y(2), ..., y(50)
t* = the modal citation-age, i.e., when that Ymax occurs
tµ = the mean citation age,[84] i.e., [sum of all y(t).t] / [sum of all y(t)] where 0 =< t =< 50
T = solution to the equation [85]
dy/dt=0 where t
is an element of the set {Real numbers}
= [ln(c) - ln(b) - d] / [c - b] and naturally
we expect T to approximately equal
t*
63. See Michael H. MacRoberts and Barbara R. MacRoberts, "Problems of Citation Analysis: A Critical Review," Journal of the American Society for Information Science 40 (Sept. 1989), 343-7; also the summaries in Liu, "Progress," 375-86, and Kelland & Young, "Citation," 86-9.
64. George A. Barnett, Edward L. Fink, and Mary Beth Debus, "A Mathematical Model of Academic Citation Age," Communication Research 16, no. 4 (Aug. 1989), 511.
65. ibid., 514.
66. ibid., 513, quoting various sources.
67. Barnett et al. merely state the rate equations and proceed directly to the equation y(t). For a more step-by-step approach to morphologically equivalent rate equations and how they produce an equation corresponding to y(t), see Ellen J. O'Flaherty, Toxicants and Drugs: Kinetics and Dynamics (New York: Wiley, 1981), 151-152; or see also Edward Batschelet, Introduction to Mathematics for Life Scientists, 3rd ed. (Berlin: Springer-Verlag, 1979), 365-7, and 368 (fig. 11.8).
68. For an introduction to such exponential functions, see Batschelet, Introduction,146-7, 336-346.
69. Note that the exponential function, whether increasing or decaying, is sometimes called a first-order because it has the generic form dx/dt = k^(xn) , where we have assigned n=1. O'Flaherty, Toxicants and Drugs, 21-2.
70. Barnett, Fink, and Debus, "Mathematical Model," 515.
71. A compartment may be defined as follows:
If a substance is present in a biological system in several distinguishable forms or locations, and if it passes from one form to another form or location at a measurable rate, then each form or location constitutes a separate compartment for the substance.
Martin Eisen, Mathematical Methods and Models in the Biological Sciences: Linear and One-Dimensional Theory (Englewood Cliffs, N.J.: Prentice Hall, 1988), 120. Similarly, Batschelet, Introduction, 344.
72. O'Flaherty, Toxicants and Drugs, 84-86, 98-101.
73. O'Flaherty, Toxicants and Drugs, 21.
74. O'Flaherty, Toxicants and Drugs, 27-8. Similarly, Edward Batschelet, Introduction, 365-7, 368.
75. K. L. Blaxter, N. McC. Graham, and F.W. Wainman, "Some Observations on the Digestibility of Food by Sheep, and on Related Problems," British Journal of Nutrition 10 (1956), 75.
76. ibid., 75. The model is also discussed in Batschelet, Introduction, 365-7, 368.
77. In the words of Blaxter et al., "Some Observations," 88-9:
The equation describing the passage of food ... may be regarded as purely descriptive and not necessarily representing underlying physiological mechanisms, since no tests to show that the constants k1 and k2 do, in fact refer to rates of transfer of digesta between the compartments of the tract specified have been made. No assumptions of the physiological validity of its constants are, in fact necessary ...
78. Sandison, "Thinking," 63. Actually this quote is slightly out of context, but his words have a wider relevance than merely to a consideration of sampling errors.
79. L. Egghe, I. K. Ravichandrea Rao, and R. Rousseau, "On the Influence of Production on Utilization Functions: Obsolescence or Increased Use?" Scientometrics 34, no. 2 (1995), 286, 289, 291ff, etc.
80. I.e., the Barnett equation y(t) may be rewritten to exactly mimic Egghe's function h(s).
81. Barnett, Fink, and Debus, "Mathematical Model," 514.
82. from ibid., 517. Not yet scanned in --- to be completed eventually
83. In principle y & t are real-numbers, continuous variables, as opposed to their experimentally derived counterparts in §8.2 below. In practice, t is a whole-number (just as in §8.2) - except for the calculation of T.
84. To be pedantic, in a continuous distribution ideally tmu = the integration of t.y(t).dt , assuming that the integration of y(t).dt = 1 . However, for this project, y(t) will actually be calculated on a spread-sheet, hence the simple summation is used.
85. The formula is the straight-forward derivative of y(t). It is also given by Barnett, Fink, and Debus, "Mathematical Model," 515. See also §10.2 below. There is a typographical error with the brackets in the analogous formula, i.e. when d=0, as derived by O'Flaherty, Toxicants and Drugs, 153. It should read : tmax = ln(ke/ka) ÷ (ke - ka)