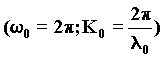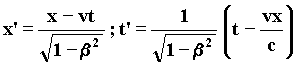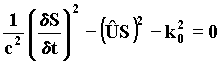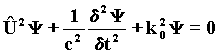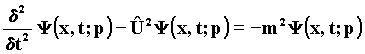|
The wave nature of inertia The waves of the particle-wave source must be considered as having a spherical symmetry, and this is the physical reality of a wave field. Let us consider now only those portions of wavefronts that propagating along the axis passing through the center of a field can be considered as plane and parallel to one another. These waves, that are temporal perturbations of the lattice of the Schild space-time, can be classically described as discrete sine waves that, being continually emitted by the source, must have a stationary description. 24) e = cos(K0 x') cos(w0 t') = u(x) y(t)
where n0 and l0 are the frequency and the wavelength of the source at rest. If the source is in motion, we shall have two different frequencies due to Doppler effect: one in the direction of motion n1 the other one in the opposite direction n2. In order to know what kind of wave will be observed from a real observer at rest, we have to apply Lorentz transformations: 25)
from which it follows that: 26) 27) K0x' = Kx - bwt w0t'= wt - bKx Consequently, the observed wave is: 28) e = cos(Kx - bwt) cos(wt - bKx) = u(x,t) y (x,t) As shown by Claude Elbaz (*), it is possible to take the wave state of particle into account and describe it as a stationary composition of plane waves in superposition of frequency n1, n2. (*) Claude Elbaz. C.R. Acad. Sc. Paris, t. 298, Série II, n¡ 13 1984. It is possible when we think of geometry, where for: dw1/w1 £ 1 ; dw2/w2 £ 1 ; dn/n £ 1 the phase: 29) S = wt - bKx of the phase wave : 30) y(x,t) = cos(wt - bKx) fulfills the Hamilton-Jacobi equation 31)
While in the field of diffraction, where: 32) Dw Dt @ 2p è DK Dx @ 2p the phase wave y(x,t) fulfills the Klein-Gordon equation: 33)
In the light of the Wave Field Theory, the Hamilton-Jacobi equation has a precise tangibly physical meaning from the wave viewpoint, that only now we can attribute to it. It virtually identifies the trajectory of a photon, describing the place of the points of the space where the wavefronts of the wave train-photon are parallel to one another. The Klein-Gordon equation would become more and more significant, if it were not falsified by the serious problem of the double solution we have to associate to it when it describes the De Broglie material waves. Indeed for: 34) w2 - p = m2 the Klein-Gordon equation has two solutions: a positive solution describing a positive momentum and a negative one that leads us to consider the possibility of the existence of negative frequencies beside the positive ones. 35)
Till now only the positive solution has provided a physical meaning. But now, in the light of the Wave Field Theory, observing the wave situation in the vicinity of the particle-wave source, we can verify the physical existence of positive and negative energy variations.
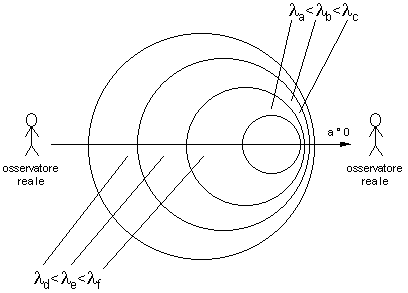
FIG.7 The change in the wave energy in the vicinity of the particle-wave source can be considered both a variation due to increment and a variation due to decrement. Consequently, according to the considerations on the relative symmetry principle we have to call “positive energy” the variation due to increment and “negative energy” the variation due to decrement. Both of them should influence the motion and rest state of the particle-wave source. Both of them can intervene in the variation in momentum in the vicinity of the particle-wave source. However, it is essential to say that regardless the type of variation, the relative symmetry principle must intervene in both cases to the same extent. On this base, we are therefore obliged to look for the possible existence of a negative energy in physics. Inertia is the negative energy. Following the Popperian philosophy, let us try a falsification of the statement and propose an experiment. Let us speed a mass up suddenly, and verify the variation in the momentum of a testing body in the vicinity of a mass, in the side opposite to the direction of acceleration of the mass, regardless the active gravitational forces, that is, subtracting the effects due to gravity.
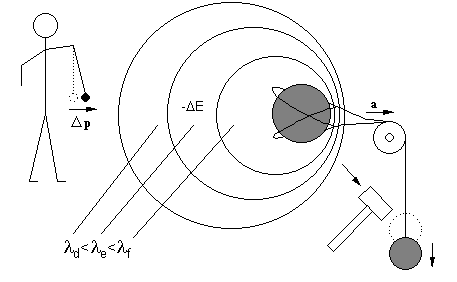
FIG.8 In the zone in which there is -E, a reduction of wavelenght has occured along with the creation of a wave energy “hole” owing to the acceleration of the mass. The relative symmetry priciple pushes the nearest masses toward the hole. It is as if in a constant-pressure atmospheric environment there were a loss in pressure, localized in a certain zone; all bodies are pushed toward that zone because of a general redistribution of pressure. The nearer the bodies to the trough are, the more they will undergo an energy action and remarkable effects. Even the mass which is accelerated is subjected to the attraction of the negative energy “hole” -DE. This effect we could improperly
impute to a force, is what we have till now called: inertia of mass. |