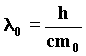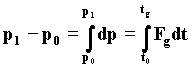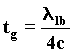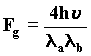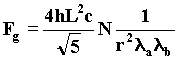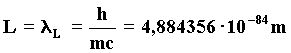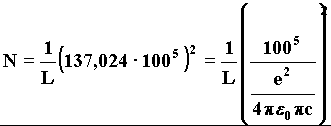Let us examine a simple physical situation in which the base units of the M.K.S. system intervene in the same way as in the Canvedish experiment.

Let us consider two spherical bodies of masses m_a and m_b considered as totally isolated in a space lacking in significant fields, both weighing 1 kilogram and being at a distance of 1 metre from each other, .

Each body emits spherical waves of rest wavelenght l_o:

Owing to the gravitational force the two isolated bodies would precipitate against each other, constantly increasing their approach velocity. In order to mantain the wave situation simple and the wavelenght emitted in any direction in the vicinity of each body constant, we have to bind the bodies with a thread having an insignificant mass so as to oppose the tendency of the bodies of attracting each other with the tension of the thread by mantaining them still in space at the desired distance.

The important points of the gravitational wave interaction are all on the straight line passing through the centers of the two bodies.

Let us observe the behavior of the wave energy along this straight line in the time which elapses from the emission of a wavefront to the following one, from each body, dividing such an interval into various times and blocking the wavefronts in such various times.

The wave energy state in the space between the two bodies is variable.

This is the conclusive observation for the wave explanation of gravitation.

As for masses having the same value, the energy in the point A is given by: 
E_ab = E_a + E_b = 2E, as much as in the point B that is symmetrical of A with respect to the center of mass of the system. It follows that: E_ba = E_b + E_a = 2E.

Actually, the observable mass outside the system along the straight line passing through the centers is given by the sum of the masses of the two bodies.

On the contrary, in the space separating the two bodies, the wave energy varies in time, oscillating in a cyclical sequence between the minimum value 1E and the maximum value 2E.

(*) A study on the nuclear mass defect will show this is not always true.

In the case a) at time t₁, the wavefronts deriving from the mass ma are intercalated to the wavefronts deriving from the mass m_b both inside and outside the system.

In the case b) at time t₂, the wavefronts propagate in opposite direction from each other and are superimposed to each other between the two bodies within the system, while they intercalate to each other outside it.

We must not forget that the elementary waves we are speaking of cannot be described as sinusoidal functions, but they must be considered as perturbation bidimensional surfaces of the Schild lattice.

When they are in a geometrical superposition, the sum of two perturbations produces nothing but another perturbation.

Two waves intercalating their wavefronts, simply produce a wave of double frequency, without having any interference phenomenon.

The variation in the negative energy -DE is a sort of stationary cyclical change that we could call: negative wave or antiphoton.(**)

(*) The amplitude of the elementary sine waves describes the value of the radius of curvature of a surface, and it never cancels out at all when it is superimposed (only in the mean point among the masses, the two waves cancel the radius of curvature).

(**) We could also call it graviton, realizing that it is not a particle but a wave train-negative photon of frequency:n = 1/t_g.

The period t_g of the negative wave must be considered as the time characteristic of the elementary wave action in the gravitational wave interaction.

It is specific for each pair of bodies and it is linked to the value of the relativistic wavelenght l₁ of the elementary wave, which is emitted by the masses m_a and m_b due to Doppler effect, when the bodies move freely toward each other. However, it does not depend on their distance.

Actually, when we take away the threads maintaining the two bodies still at the desired distance, after a time t_g the momentum of each body will be changed from zero to: p=mv.

Along the straight line passing through the centers, the velocity of waves c is constant, while the time of the energy-wave variation t_g varies in the space among the bodies.

On the contrary, the ratio t_g/l₁,whose constant value is: 1/4c, remains unchanged during the approach of masses.

The first impulse for each body is given by the variation in momentum in time t_g. (*)

the nonrelativistic momentum of the mass m_a is:

p_a = m_av

(*)Let us discuss about integrals and differentials as if we were in a continuum, seeing that we consider the dimensional quanta of a discontinous set very small. However, the question should be coped with after analysing the finite differences.

Therefore, the gravitational wave force, which does not depend on the distance among the masses yet, has a first component:

In order to find the second component, we have to take the hypercubic lattice of the Schild space-time and its perturbations into account, considering the importance of the radius of curvature of the elementary waves establishing the effectiveness of the relative symmetry principle in the gravitational interaction.

Let us apply the formula 15) for l_a = l_b in order to obtain the velocity of the waves that are parallel to one another outside the system of the two bodies, and which will inversely depend on the Gaussian radius of curvature of the wavefronts portions.

K is the factor of proportionality with dimensions [L²].

Given the distance quantization and the following surface quantization, the unitary surface parameter that is proportional to the velocity v is: K=N L², where N is the number of the surface quanta L² of the parallel "effective" wavefront.

When K is substituted in the formula of the velocity v , it follows that:

We obtain therefore the second factor that in the formula F_g gives :

There are two unknowns in this formula: the discrete elementary lenght L, and the number N of the discrete elementary surfaces forming the effective wavefronts, which constitute the wave trains activating the relative symmetry principle.

Let us formulate the "ad hoc" hyphothesis, we shall try to justify in the next chapter,( partly depending on considerations on the symmetry of the domains of natural constants) that a "reasonable" value of the discrete elementary lenght depends on the absolute magnitude of a terminal mass.

for the unitary l

We put forward a hyphotesis (we will estimate afterwards its soundness) on the value of the discrete lenght equivalent to the dimensional quantum L, through which we can calculate the value of the number N of the effective wavefronts in the wave formula of gravitation.

When we take the unitary parameter N from the experimental findings of F_g, we shall obtain the following result:

(where 1/L is the pure number showing the number of the linear quanta L in 1 meter)

The number N could seem at first sight lacking in physical meaning, but if it is resolved into factors, it will became of fundamental importance.

Where the number 137,024 being too similar to the inverse of fine-structure constant, is identified with it.

If such an identification were confirmed by other elements and considerations, we should have a first reasonable element so as to link elementary waves and their gravitational action to electromagnetic waves and to interactions among electric charges.

Afterwards, we will be able to discuss about sound subjects supporting this thesis. Now, we can already estimate the capacity of the model to describe gravitational interactions.

Through it we can follow the various quantum phases of the gravitational wave action, highlighting the "whys", tightly connected to gravitation, apart from the "wherefores".