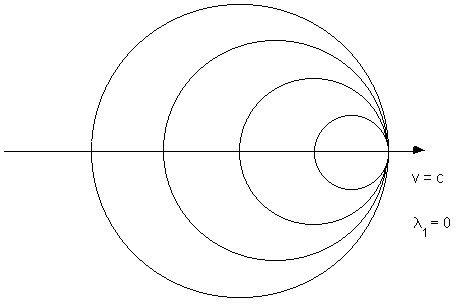
We know that the rest wavelength of an electron decreases owing to Doppler effect when the electron mass is accelerated at velocities approaching c:

How long will its wavelength go on to decrease?

As to the relativistic increase in mass, the question is as much as to wonder: till which value can a mass increase, if accelerated at velocities approaching the velocity of light?

.

Could a mass ever reach the velocity of light?

That is as much as to wonder: is it possible for the wave source to reach the velocity of the waves it produces?

If it were possible, it would mean that the wave source produces waves whose wavefronts are superimposed one upon another, and they would have therefore a null wavelenght.

It cannot certainly occur in the Wave Field Theory. In such a theory it does not make any sense to speak of a mass having a null wavelenght. The same goes for speaking of infinite mass in any other physical theory.

Nor does it make any sense to consider in the De Broglie wave theory any mass to which a wave train with a null wavelength is associated.

The questions find a common answer in the discrete space-time and in its length quantization.