|
On the basis of the wave model of beta decay, which has described the variations in the spherical involute organization, we can now deduce by experiment a possible wave structure of particles with short life-time: let us consider some of them as resonances of the spherical Involute-electron and others as variations of the model of neutron. We must reconsider the formulae of mass that in 1952 (5) Y. Nambu tried to apply for calculating the particles’ mass, by taking the electron mass as a base. Today these formulae, which at the time did not make any sense and had some embarrassing holes, have been rediscovered with the wave model of particles, and they try to fill the void they had left. Nambu knew by experience, without being supported by any theory, that particles with mass were the product of the electron mass multiplied by the inverse of fine structure constant: 137, and for n Î N or for n = quotients of integers.Therefore the muon mass would be: 85)
and the pion mass: 86)
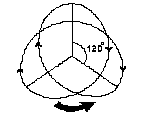
But there was no particle with a mass derived from n =1. It was clear that no theory could support his numerical mechanism. The wave field theory bases itself on the same method which is more effective in describing the particle’s masses and bridging the gaps. The wavelength le, which is a characteristic of the electron mass, is the basis for the calculation of the wavelengths of the unstable particles' masses. For several minutes the electron’s resonance wave remains in neutron in an anomalous state that can justify the added mass of neutron compared to the sum of the masses of its components: proton and electron. Therefore, the first variation in the electron mass occurs in neutron with: 87) men = me 3/2 that has the wavelenght: 88) len = le 2/3 It is explained referring to the figure of precession with three lobes derived by neutron linked to the appearence of deuteron. Although the resonance orbit in precession is not a closed path, it has the same possibility of forming the involute; but in this case it is an unstable compound involute producing a wave variation which introduces a retrograde component into the spherical involute.
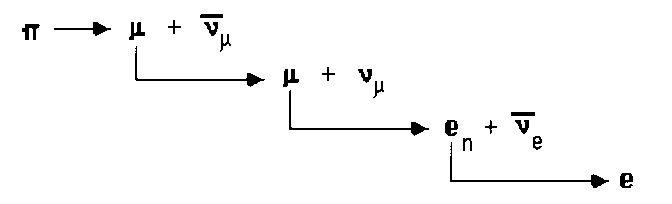
FIG. 27 Precession of 120° for the retrograde rotation. This type of variation is the basis for the comprehension of the model of the spherical involute which justifies properties and decay of unstable particles. As for muon, the wavelength, after evolving as in neutron, makes a sudden jump and becomes 137 times smaller. The reason for this jump is not clear yet, but only the Wave Field Theory, which enables us to verify the wave nature of fine-structure constant in atomic emissions, (as we shall see later) unlike other theories, is likely to come to a logic, consistent, causal understanding. In order to better understand the particle’s sequences, it is useful to use a formula which links a condition to another through the interval of a numerical sequence expressing the various passages; but we have to observe the muon as a product of pion decay. In the series of decays there is a new particle, never suspected before, deriving from the transformation of the first free electron into the electron of neutron. 89)
The second passage is between the electron of neutron and muon. 90)
The third passage is between muon and pion.
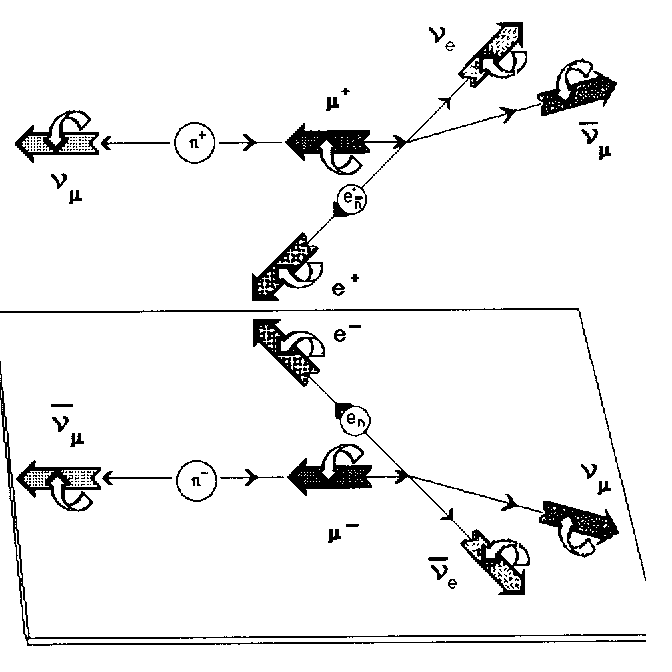
These are the wavelengths of the various particles that we find in cascade during pion decay. Now, there is the possibility for n =1 to justify the existence of a neutral pion composed of two wave trains (the two resultant photons) of wavelenght = 2lp which temporarily coexist on the same resonance orbit. It is useful to know that by increasing the value n, we justify other mesons. Moreover, it is possible to apply the model of neutron on adrons. Let us describe the phenomenon of pion decay according to the standard interpretation, adding the phase of beta decay, and emphasizing the characteristic chiralities of the reflected phenomenon.
FIG 28 The antineutrino of electron in the
reflected phenomenon is identified with the antineutrino of the neutron
beta decay. |
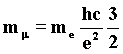
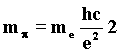
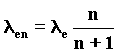 for n=2
for n=2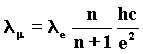 for
n=2
for
n=2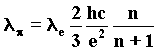 for
n=3
for
n=3