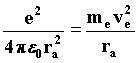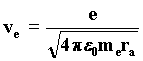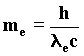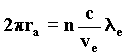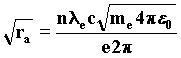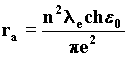Let us consider that an electron moving in space can be described by a wave train moving along a tube with the axis coinciding with the electron's direction of motion. Firstly, it describes it as depending on the non-relativistic wavelength of the waves preceding it along its trajectory.

According to classical electrodynamics, the Rutherford atom maintains an equilibrium between the electric force binding proton and electron together and the centrifugal force necessary for the electron to exist in the vicinity of the proton.

From this equation we obtain the value of the velocity that the electron needs to remain in a stable orbit.

The resonance condition necessary for the waves needs an integer of such waves moving in a closed orbit.

We can reach such a condition through the wave interpretation of the principle of least action which, in classical mechanics, influences the motion of any body.

Infact, according to classical mechanics, a mass in motion in the space between two points tries to develop its own trajectory depending on the principle of least action according to which the product of the body’s mass results as least as possible owing to the velocity attained and the distance covered.

Let us suppose that in an orbital path S is the momentum. It follows that:

S = m_ev_e2pr_a

where r_a is the radius of the covered orbit and v_e the electron velocity.

From Planck we know that every action is composed of entire multiples of action quanta h ; therefore S = n h and consequently:

Substituting the electron mass with its wave equivalent:

we have :

With the wave interpretation, we obtain the resonance law from the condition of least action.

It describes the length of the orbit followed by the electron about the proton depending on the number of wavefronts in the orbit, which is given by the ratio of the velocity of waves c to the velocity of the wave source-electron.

Such a ratio must certainly be an integer; we find it by substituting in the last formula the velocity v_c taken from the Rutherford equilibrium condition, from which we deduce the value r_a.

Substituting once again the electron mass with the wave formula n=1, we obtain the wave equivalent of the Bohr radius of the first orbit of the atom of hydrogen.

But now the wave description paves the way for a wave interpretation of fine-structure constant, derived causally by the relativistic conditions of the phenomenon.