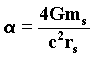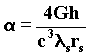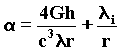The wave interpretation of General Relativity

The shift velocities of the temporal perturbations inside the hypercubic lattice, in the Schild discrete space-time depend on the fields of curvature the perturbations meet during their propagation. This involves the wave interpretation of field in the explanation of the interaction of light with gravitational fields. We can introduce the wave interpretation of the formula describing the angle of deviation of light from the solar mass.
 
47)



Describing from the wave point of view the ms solar mass having m_s, as a radius  r_s,  it follows that:

48)



In the wave language the angle of deviation of the photon-wave train is proportional to the wave number of the deviant mass and inversely proportional to the radius of the mass waves interacting with the incident photons.

The plane waves of the photon having a great radius of curvature and little energy are influenced by the spherical waves system of the Sun, having a  smaller radius of curvature and great energy . Besides the G.R. description, the deviation should be also proportional to the wavelength of the diverted photon, since there are two wave agents acting in the phenomenon: the waves of the photon having li as a wavelenght and the mass waves of the Sun.



(Till now, a dependence from the wavelenght of photon has been neither verified nor considered; it depends on the exiguity of the angular deviation effect observable with macroscopic bodies, that in the case of the solar deviation would have increased the angle of deviation only by an insignificant umpteenth decimal).

In order to understand the phenomenon in its possible variations, it is necessary to consider the role of the radius of deviation when the involved masses get smaller.

We can make a complete wave description of variables by adding a term to the 48, and generalizing for any mass.

  49)



We can immediately notice that the added term ( l _i / r ) is not really significant in determining the value of the angle of deviation, when in the phenomenon great deviant masses having a great radius are involved. On the contrary, when we carry out the experimentations with smaller and smaller masses having shorter and shorter distances from the centre of the wave field, the first term loses importance while the added one becomes predominant.

When we experiment the effect of the deviation of light from the matter, we immediately meet with a macroscopic deviation effect that in Optics is called Diffraction.

  

 
The optical diffraction from a thin edge is an example of deviation of light that on a small scale can be compared to the solar deviation.

According to the wave hypothesis of field, in the diffraction from a thin edge, the obstacle placed on the path of the waves of the photon travelling in the light ray gives out a series of wavefronts, that create all around the profile of the obstacle a field of waves similar to the obstacle in its shape.

This field of waves derives from the spherical waves given out by all the elementary particles constituting the matter of the obstacle at a subatomic level.
If the obstacle is formed by the profile of an upright blade, it gives a wave of semicylinder shape.

Being nearby the edge, the experimental wave situation is, on an inferior scale, quite similar to the one verifying in the deviation of light from the solar mass; but, in the last one there are some quantitative differences underlining the validity of the qualitative considerations on the importance of the smallness of the radius of the deviant waves.

The angle of deviation of light imposed in the diffraction phenomenon from an edge is, in optics, more marked than in the phenomenon described by the general relativity. There are mainly two changing data:
 

• The frequency given out by the edge of the deviant obstacle is much smaller than the one given out by the Sun. Therefore, its wavelength is much greater.
• The radius of the waves given out from the edge with which the light comes into contact during its passage near it, is much smaller than the radius of the spherical waves given out by the Sun, which start from its surface and have at least the same radius as the Sun itself.

The first conclusion we can draw is that, even if the size of the angle of deviation of light imposed by the general relativity seemed to depend on the mass value of the deviant body, the radius of the mass field is much more determining since it is the deviant cause.

Therefore, we suppose that the formulas of the general relativity must be considered only as first approximations of the true law, in which the really determining factor is the smallness of the radius of the mass waves involved in the diffraction phenomenon.

Yet, even this phenomenon gives only qualitative confirmations. In order to find a quantitative analysis, it is necessary to examine other phenomena of interaction between matter and light, in which the radius of the mass waves is still small, and it is even more determining in putting in evidence the action of the form waves in the orbit of the photons of light.

The determining and definitive phenomenon happens in the adverse field: the Compton effect.

If this was true, it would mean that it is possible to lead the General Relativity within the interactions of the radiation with the elementary particles, by using the wave description of field for the wave interpretation of the key phenomena of the Quantum Mechanics.