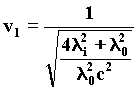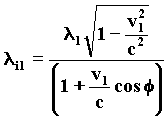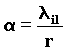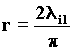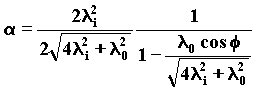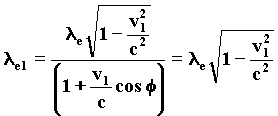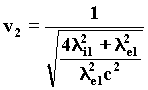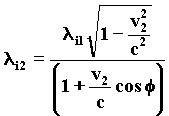The wave description of the Compton effect
 We can verify the hypotheses and the laws deriving from the new wave theory, by using the Relative Symmetry Principle and the wave changes in the General Relativity, for a new purely wave interpretation of the simplest phenomenon of interaction between matter, in the form of elementary particle (electron), and the most elementary radiation (photon) in the Compton effect.

Let’s observe, in four times, an ideal experiment of Compton interaction with a photon having li as a wavelength
l_i = 1•10^-10 m diverted by 90° by a free electron, in a space deprived of significant fields.

1) the photon gets closer to the source of the field of the electron, and its energy is added to the one of the waves of the field of the electron in the A zone:

50)

Fig. 11

Because of the wave variation, the Relative Symmetry Principle obliges the electron to the motion, imposing the v₁, velocity on it.
from 15) we draw the  v₁, velocity. It follows that:

51)

Let’s consider the frame of reference of the electron-source of waves that  moves with the v₁ velocity. Observing the incident photon, we notice a decay due to Doppler effect, as resulting from the following formula, where the angle of incidence Ø of the photon compared to the direction of the velocity of the electron is p.

52)

After the decay, the photon is diffracted a = p/2, by the spherical field of waves of the electron, in compliance with the G.R. modified formula, considering the first part insignificant.

53)

for          

The r radius is the least distance from the centre of the particle-source of spherical waves, which is crossed by the incident photon before being diffracted. This radius plays a decisive role in the whole following study, introducing the descriptive possibilities of the theory through the new wave interpretation of the General Relativity.

Before that, a phenomenon of pure and simple deviation of the plane wave train-photon takes place from the wave field of the electron. Since the electron hasn’t had time to accelerate (as we have seen for the solar deviation), it limits itself to the diffraction of the photon, maintaining its energy unchanged. The phenomenon is actually experimentally observed when the incident light ray is formed by several photons. It gets the presence of a component of the diverted radiation, with the same angle, which has the same energy of the incident radiation, and isn’t therefore subject to decay.

As shown by the following formula drawn by the v₁, velocity and from l_i1where the variables of the phenomenon play their role:

54)

Considering the wavelength of the incident photon and the wavelength of the deviant particle, we can foresee the maximum angle of deviation of the photon, (and this has an experimental importance), and know the least radius of the curve described by the photon all around the centre of the wave field of the diffracting particle.

Fig. 12

Because of the acquired velocity, the field of waves of the electron is modified by the transverse relativistic effect. So, after undergoing a first decay, the photon triggers a new push effect, in compliance with the Relative Symmetry Principle (*), and develops a new momentum in the electron (where the transverse mass of the electron enters) having a direction that is orthogonal compared to the previous one.

(*) That since now will be called R.S.P.

The transverse relativistic wavelength of the electron (that justifies the existence of the transverse mass of Relativity) is:

55)

If it is introduced in the R.S.P. formula, because of the push given by the photon having l_i1, as a wavelength, it allows the electron to have a v₂  velocity that is orthogonal compared to the previous one:

56)

57)

Compared to the electron-source of waves, which moves with v₂, velocity, the diffracted photon further decays because of the Doppler effect, as given out by the electron, and its final wavelength becomes:

58)

The diffracted photon has as a whole:

59)

Dl_i = l_i2 - l_i1

while the electron has reached the velocity: v_e = v₁ + v₂ (*)

(*) The sum of these two velocities is not a simple vector sum. Lyevelin Thomas (* *) showed that a Lorentz transformation with v₁ velocity, followed by a second transformation with v₂ velocity, in another direction, doesn't lead to the same inertial reference reached by a single Lorentz transformation having v₁ + v₂. as a velocity.

(* *) (H. A. Kramers, Quantum Mechanics, New York 1957)